Homework Help Overview
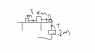
The problem involves a pulley system with two particles of masses m and 2m on a smooth horizontal table, connected by a string that hangs over the edge and supports a mass of 3m. The objective is to determine the acceleration of the mass 3m.
Discussion Character
Approaches and Questions Raised
- Participants discuss the interpretation of the problem, particularly regarding the acceleration of the different masses and the setup of equations. There are questions about whether all masses accelerate in the same direction and how to account for the mass of the pulley.
Discussion Status
Participants are exploring various interpretations of the problem setup and discussing the relationships between the accelerations of the masses. Some have suggested that the problem provides enough information to establish constraints, while others express uncertainty about the clarity of the problem statement.
Contextual Notes
There is a lack of explicit information regarding the configuration of the pulley and the string, leading to differing interpretations. Some participants note that the absence of a diagram may contribute to confusion about the physical setup.