Homework Help Overview
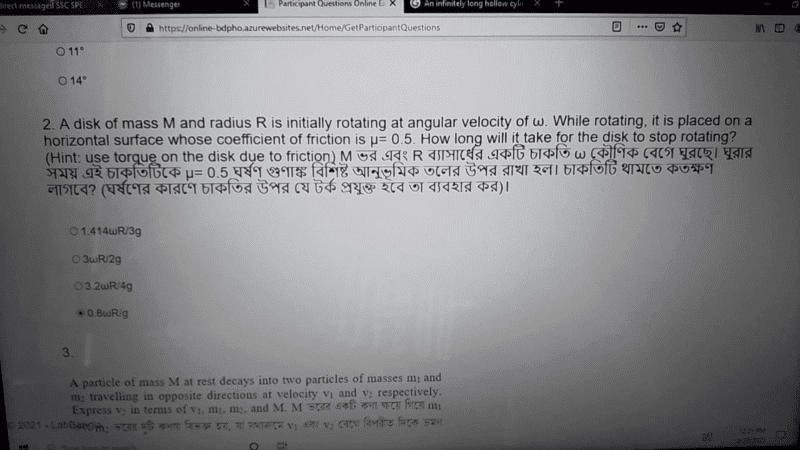
The discussion revolves around a physics problem related to the rotational motion of a solid disk, specifically focusing on how long it takes for the disk to stop rotating. Participants are analyzing the moment of inertia and angular acceleration in the context of this problem.
Discussion Character
- Mathematical reasoning, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants are attempting to identify errors in the original poster's calculations, particularly concerning the moment of inertia and the substitution of values. Questions are raised about the correct value of the coefficient of friction and the implications of algebraic errors in the calculations.
Discussion Status
There is ongoing clarification regarding the calculations and assumptions made by the original poster. Some participants have provided guidance on identifying specific errors, while others have noted the difficulty in reading the original poster's work. The discussion is active, with multiple interpretations being explored, but no explicit consensus has been reached.
Contextual Notes
Participants have pointed out that the original poster's handwriting is difficult to read, which may be contributing to misunderstandings. There is also a focus on the importance of correctly identifying the moment of inertia for the solid disk in the calculations.
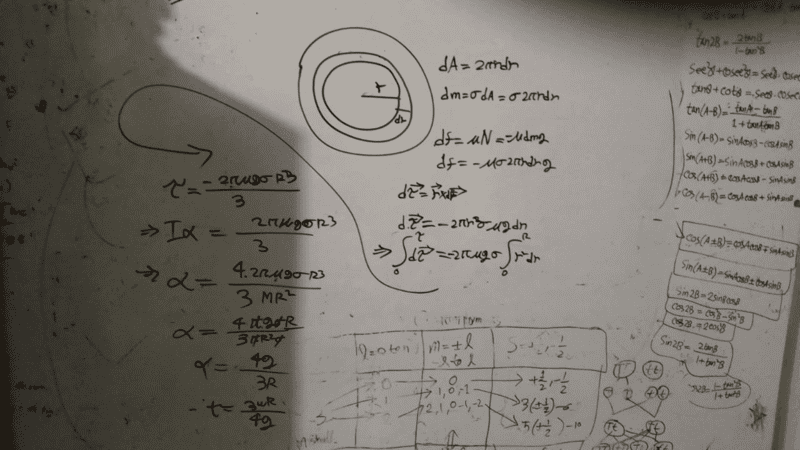 for
for