hojoon yang
- 8
- 0
Hi
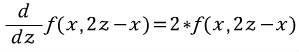
I understood above differential
## typo. RHS= 2*f ' (x,2z-x)
but, what is answer of below equation?
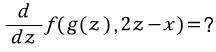
is this right?
f ' ( g(z),2z-x) * g' (z) + f ' ( g(z),2z-x) *2
I understood above differential
## typo. RHS= 2*f ' (x,2z-x)
but, what is answer of below equation?
is this right?
f ' ( g(z),2z-x) * g' (z) + f ' ( g(z),2z-x) *2