How the power transfers across the Ideal Transformer

[jim hardy]

A picture to go with Electrician 's observation

Where would

flux be the biggest

?

Where would flux per amp be the biggest ?

 

[tim9000]

Hi all, thanks for the replies.

Volts per turn would be constant VP/N ... and for sine waves that's constant flux. Well, as constant as VP is...

Do I interpret you correctly as: 'As long as the primary Vp sine excitation is constant, there will be a (90^o lagging) sineusoidal flux of constant maximum amplitude and frequency, regardless of secondary load'?

On your curve I'd say it'd be at zero, but I was thinking more of a BH curve like this:
https://upload.wikimedia.org/wikipe...Permeability_of_ferromagnet_by_Zureks.svg.png
Where the point would be μ_max

Again, you've leapt right over some thinking steps.
What model are you using?
Usually one varies only one parameter at a time(and calls that one independent), observes another(calling it dependent) , and derives a third as function of those two

Spot on critisism, hopefully soon I'll learn to stop skipping mental steps and you're exactly right, I do have trouble sometimes separating things into just one dependant variable, I'll take that onboard.
Ok using the model (with Rp and Xp still present):
https://www.physicsforums.com/attachments/transformer-jpg.84964/
So using that BH curve at the point of μ_max, with respect to: L_M= μN²A/Length = N²/reluctance
Assuming we had some arbitrary constant cross sec area and number of turns, then μ is higher than when opperating at the knee point,
So I'd conclud that the inductance Lm is bigger and so I_o is smaller. But since also L_m = Φ*N/I_o than for the dependant variable:
Φ = L_m*I_o/N
I'm not quite sure if this stays the same or not? (Given Lm has risen and Io has shrunk) So I can't really compare how the TX differs from use at the knee point...maybe I'm just tired atm...(packing boxes to move/tending to yard all day)

You're speaking of a "slope". When such words are used, it's usually in a discussion about "small signal" performance.
Yes, when the slope of the BH curve is steep, the incremental flux will be largest there, but not the overall ("large signal") flux.

My use of the word slope is due to my lack of technical discipline/awareness.
Could you please elaborate on 'small signal performance'? Sounds interesting: By incremental flux do you mean like the rate of increase of flux? (but by 'large signal' do you mean like the end result peak flux?)

In the model , what have you fixed for a starting point? VP ?

For pf=1, what is magnitude of magnetizing current? VP/XM ?
So for good PF you'd want XM as large as practical ?
To maximize XM , i suppose you'd maximize inductance XM/ω , okay to call it LM ?
if LM= μN2A/Length

Yeah so Vp is a fixed sin excitation (I know frequency and peak excitation voltage affect where you are regarding saturation); yeah so I was thinking if you wanted the PF to be near 1, you'd need to have almost no Rp and Xp, Xm would be really high so all the current went through the ideal TX and I_o would be almost non existant. But the question was relating this to the opperating point on the BH curve, I suppose what I was eluding to is that if you're opperating further back down the left side of the curve is I_o smaller?

 

[jim hardy]

Do I interpret you correctly as: 'As long as the primary Vp sine excitation is constant, there will be a (90o lagging) sineusoidal flux of constant maximum amplitude and frequency, regardless of secondary load'?

Yes, look at your model that is the magnetizing current I_M .

but I was thinking more of a BH curve like this:

So using that BH curve at the point of μmax, with respect to: LM= μN2A/Length = N2/reluctance
Assuming we had some arbitrary constant cross sec area and number of turns, then μ is higher than when opperating at the knee point,

What i think is the point of confusion comes from imprecise terminology in the industry.
A transformer core doesn't operate " at " a point on the curve.
That is a DC curve and only shows one quadrant.
The transformer flux is a sine wave swinging between some positive and negative value of flux every line cycle.
In my BH curve that'd be upper right and lower left quadrants.
Yours omits the lower left, so just imagine it's there.
Flux swings from above to below the horizontal line, mmf swings left and right of the vertical one, at line frequency.
When we say a transformer is operated "at" certain flux we usually mean that's the peak flux. value.
Flux is a sine wave with that peak value.
So the core is operated not "at" but "out to" those two peak values, and flux crosses every point in between them 120 times a second.
Flux 'walks the line' , the gray one, crossing all points between its peak values twice per line cycle ..

The blue permeability line in your BH curve is just slope of the gray flux line, as electrician noted.
Its purpose is to demonstrate iron's nonlinearity
which is why magnetizing current gets that pesky distortion as flux traverses the knee.

Yeah so Vp is a fixed sin excitation (I know frequency and peak excitation voltage affect where you are regarding saturation); yeah so I was thinking if you wanted the PF to be near 1, you'd need to have almost no Rp and Xp, Xm would be really high so all the current went through the ideal TX and Io would be almost non existant.

Applause ! Well said.

But the question was relating this to the opperating point on the BH curve, I suppose what I was eluding to is that if you're opperating further back down the left side of the curve is Io smaller?

You're not operating at a point you are operating between two points positive and negative peak.
In most power transformers those points are symmetric about zero.

Variations in incremental permeability will more affect the shape of magnetizng current than its amplitude..

Its amplitude is set primarily by how far out the B axis you push the core.

A search on "Barkhausen effect" might help cement the B-H curve in your mind.

 

[tim9000]

The transformer flux is a sine wave swinging between some positive and negative value of flux every line cycle.
In my BH curve that'd be upper right and lower left quadrants.
Yours omits the lower left, so just imagine it's there.
Flux swings from above to below the horizontal line, mmf swings left and right of the vertical one, at line frequency.
When we say a transformer is operated "at" certain flux we usually mean that's the peak flux. value.
Flux is a sine wave with that peak value.

Now that is food for thought, I suppose that is one of those things I probably did realize at one point but since I'm not working in industry yet my synapses haven't solitified.

Ok, so the knee point is the peak flux point, it doesn't really opperate there. So does this mean that the famous X_m we've been talking about is the peak magnetising impedance?
Right so about the whole "peaky distorted" magnetising current when it goes nonlinear: so the flux will have a nice sineusoidal shape up as we run up (or down, +/- quadrants) the BH curve, because BH is kind of linear there and in a linear core the flux will have the same shape as excitation supply? But when the flux wants to follow the shape of the supply (90 deg lag) but it can't because the core is saturating, the flux sort of flattens off.

I'll be keen to hear your (always appreciated) response/evaluation of my development.

Hey if you're so inclined, another helpful and nice FP'er has been helping me on this circuit thread and I was wondering if you had anything to weigh in on about it:
https://www.physicsforums.com/threa...-transformation-question.820851/#post-5153065
if not, don't worry.

Thanks heaps Jim

 

[jim hardy]

Ok, so the knee point is the peak flux point, it doesn't really opperate there. So does this mean that the famous Xm we've been talking about is the peak magnetising impedance?

I'd say the mean..

Right so about the whole "peaky distorted" magnetising current when it goes nonlinear: so the flux will have a nice sineusoidal shape up as we run up (or down, +/- quadrants) the BH curve, because BH is kind of linear there and in a linear core the flux will have the same shape as excitation supply? But when the flux wants to follow the shape of the supply (90 deg lag) but it can't because the core is saturating, the flux sort of flattens off.

I'll be keen to hear your (always appreciated) response/evaluation of my development.

You're getting there.
Back to stepwise thinking.
What have you selected for your independent variable? The one you control ?
I like to use voltage.

Right so about the whole "peaky distorted" magnetising current when it goes nonlinear:

"it" meaning the BH curve, so each incremental bit of flux beyond the knee requires a disproportionate amount of magnetizing current

so the flux will have a nice sineusoidal shape up as we run up (or down, +/- quadrants) the BH curve,

If we chose voltage for our independent variable then flux must equal its derivative , whoops, integral _jh sine and cosine have same " sineusoidal "shape

because BH is kind of linear there and in a linear core the flux will have the same shape as excitation supply?

Have you leapt again ?
"excitation supply" voltage? Their respective shapes are set by math - derivative function.
If the core is linear, MMF will have same shape too because reluctance is constant.
MMF is amp turns. So the the BH curve sets the relation of current to flux , not the relation of voltage to flux.

But when the flux wants to follow the shape of the supply (90 deg lag) but it can't because the core is saturating, the flux sort of flattens off.

Again, what did you start with as independent variable?
In ideal inductor(or transformer) Flux and Voltage must keep that derivative relationship.

When the core begins to saturate , more magnetizing current must flow to push flux through the core which is becoming increasingly reluctant to accept it.

Again you have switched independent variables on me - from voltage to current to flux and back.

Here's a real inductor with not-sinewave excitation.
Top trace is 20 milliamp peak to peak triangle wave current.
We controlled current as our independent variable.
Bottom trace is induced voltage .
Observe voltage approximates d/dt of current
corners are rounded and top is not quite flat because iron is imperfect - eddy currents and creep(as in barkhausen)

flux was too small to get anywhere near saturation
and this was only 3 hz

It is not clear to the eye that a derivative relation exists when looking at sine waves
this 'scope trace was an eye opener for my technician (who questioned much like you do)

what would voltage do if we reached saturation? Remember we control current...
i think voltage would taper off to zero between current peaks.
because flux would flatten instead of following mmf.

Learn to think in terms of slope - that's derivative...

 

[tim9000]

I'd say the mean..

mean, as in you'd calculate it using RMS?

You're getting there.
Back to stepwise thinking.
What have you selected for your independent variable? The one you control ?
I like to use voltage.

Say we were using a transformer. Keeping frequency of the supply and secondary load constant, but varying the supply amplitude: the flux will have a nice sineusoidal (derivative of EMF) shape up as we run up (or down, +/- quadrants) while the voltage amplitude is low, because the maximum B is still in the linear region of the curve, and when the core is linear the flux will/can have the same shape (derivitive of supply) as the supply voltage because the flux is free to do what it likes. But as I increase the amplitude of the supply B will start to peak encroaching in the nonlinear region, and as it does, the rate of increase of the flux can't keep up with the supply and it flattens off (so the current drawn is larger and the secondary excitation voltage is much smaller).
Is that a little bit better?

If the core is linear, MMF will have same shape too because reluctance is constant.
MMF is amp turns. So the the BH curve sets the relation of current to flux , not the relation of voltage to flux.

Aah, good point, so better to think of it as Excitation voltage -> Mag Current -> Flux

It is not clear to the eye that a derivative relation exists when looking at sine waves
this 'scope trace was an eye opener for my technician (who questioned much like you do)

what would voltage do if we reached saturation? Remember we control current...
i think voltage would taper off to zero between current peaks.
because flux would flatten instead of following mmf.

Good example to highlight your point, I should keep derivative in mind
Yeah so you're saying if you were saturating that inductor there derivative action couldn't take place, or would be so small that the EMF would be near zero.

One other question:
-Do you understand what The Electrician was saying?

"
The Electrician said: ↑
You're speaking of a "slope". When such words are used, it's usually in a discussion about "small signal" performance.
Yes, when the slope of the BH curve is steep, the incremental flux will be largest there, but not the overall ("large signal") flux.

"
My use of the word slope is due to my lack of technical discipline/awareness.
Could you please elaborate on 'small signal performance'? Sounds interesting: By incremental flux do you mean like the rate of increase of flux? (but by 'large signal' do you mean like the end result peak flux?)

I gather you didn't really have a differing opinion on that other thread, that's cool.

Cheers Jim!

P.S I'm moving house tomorrow and they have to send a technician out to set up the internet and phone so I may be offline for some time :-|

 

[jim hardy]

mean, as in you'd calculate it using RMS?

rms volts / rms amps

Say we were using a transformer. Keeping frequency of the supply and secondary load constant, but varying the supply amplitude: the flux will have a nice sineusoidal (derivative of EMF) shape up as we run up (or down, +/- quadrants) while the voltage amplitude is low, because the maximum B is still in the linear region of the curve, and when the core is linear the flux will/can have the same shape (derivitive of supply) as the supply voltage because the flux is free to do what it likes

whatever it has to do to remain derivative whoops make that integral of the EMF that you applied._{( i fixed that in previous post too )}

But as I increase the amplitude of the supply B will start to peak encroaching in the nonlinear region, and as it does, the rate of increase of the flux can't keep up with the supply and it flattens off since flux cannot flatten out because to do so would destroy the derivative-integral relation between itself and sinewave applied voltage V_P, (so the magnetizing current drawn must rise to provide MMF sufficient to drive flux up and if necessary over the knee of the BH curve. ) is larger and the secondary excitation voltage is much smaller).

Is that a little bit better?

it was until you said this

and the secondary excitation voltage is much smaller).

You reverted to throwing out words without thinking.

Aah, good point, so better to think of it as Excitation voltage -> Mag Current -> Flux

Independent variable -> dependent variables

Yeah so you're saying if you were saturating that inductor there derivative action couldn't take place, or would be so small that the EMF would be near zero.

Did you think that through before hitting reply?
Do you not proofread and check against prior progress ?
Derivative action MUST take place, that's Faraday's explanation of what Mother Nature does.
Since in that picture the controlled variable is current which = mmf
unlike the prior setups where we controlled EMF
were i reaching saturation
flux would stop increasing,
hence its derivative would become zero ,
so voltage would become zero too,
because derivative of something that's not changing, ie constant, is zero.

One other question:
-Do you understand what The Electrician was saying?The Electrician said: ↑
You're speaking of a "slope". When such words are used, it's usually in a discussion about "small signal" performance.
Yes, when the slope of the BH curve is steep, the incremental flux will be largest there, but not the overall ("large signal") flux.

incremental inductance N ΔΦ/ΔI

I gather you didn't really have a differing opinion on that other thread, that's cool.

That type problem is just really tedious algebra .

It's iterative - start combining circuit elements at one end and keep on going.

I gave up beating my head with them .

 

[tim9000]

rms volts / rms amps
whatever it has to do to remain derivative whoops make that integral of the EMF that you applied._{( i fixed that in previous post too )}
it was until you said this

You reverted to throwing out words without thinking.
Independent variable -> dependent variablesDid you think that through before hitting reply?
Do you not proofread and check against prior progress ?
Derivative action MUST take place, that's Faraday's explanation of what Mother Nature does.
Since in that picture the controlled variable is current which = mmf
unlike the prior setups where we controlled EMF
were i reaching saturation
flux would stop increasing,
hence its derivative would become zero ,
so voltage would become zero too,
because derivative of something that's not changing, ie constant, is zero.
incremental inductance N ΔΦ/ΔI
View attachment 85302That type problem is just really tedious algebra .

It's iterative - start combining circuit elements at one end and keep on going.

I gave up beating my head with them .

sorry that was a bad reply, I was rushed because I was just about to move out. I'm still without internet my ISP gave me a wireless dongle until the adsl is finally working.
So I'm a bit warey of drop-out so this post will unfortunately be a bit rushed too, sorry:
When you're taking one as an independant variable, you'd have to consider the internal impedannce and internal voltage or current source wouldn't you? such as to maintain voltage you'd have to think of the circuit as a voltage divider and modulate the internal source voltage accordingly? and to have the current as the independant variable you'd need to measure the current and vary the source current accordingly?

I kind of forgot or lost sight of the significance of the derivative action and Faraday's realisation of it as the main event.

I know that when you drill too far down scientific laws are based on observation not an underlying reason, so this might be beyond the scope, but I'm still puzzeled about what the actual physical explanation of how that "derivative" action actually takes place, and how the BH curve affects that. What I don't understand is that it has always seemed to me that the flux is either the integral of EMF or not, like a binary is or isn't relationship. But that doesn't seem correct because the curve isn't really like that. To put it another way as the curve starts to go over the knee non-lineary saturating it's not like it can be 'a bit of the integral'. Do you understand my confusion?

To illustrate the example, picture the magnetising current wave form distorting from a sinusoid to one with steeper peaks, or the flux sinusoid with shallower peaks, like it's flattening off. The derivative action is still there, just not 'fully'. Still has some shape of being the derivative, but a bit deformed...sorry I'm rushing this reply

thanks!

 

[jim hardy]

When you're taking one as an independant variable, you'd have to consider the internal impedannce and internal voltage or current source wouldn't you? such as to maintain voltage you'd have to think of the circuit as a voltage divider and modulate the internal source voltage accordingly? and to have the current as the independant variable you'd need to measure the current and vary the source current accordingly?

you have control of the independent varible by hook or by crook. Remember analysis is a thought process not hardware. When you do a physical experiment you need hardware that'll replicate your thought process.

I kind of forgot or lost sight of the significance of the derivative action and Faraday's realisation of it as the main event.

volts per turn equals rate of change of encircled flux.

but I'm still puzzeled about what the actual physical explanation of how that "derivative" action actually takes place, and how the BH curve affects that.

BH curve relates flux to mmf and mmf is ampsXturns. No derivative involved.
Have you forgot that Φ = μ X μ₀ X N X I X A /l_{ength of path} ? See any derivatives in that ?

What I don't understand is that it has always seemed to me that the flux is either the integral of EMF or not, like a binary is or isn't relationship. But that doesn't seem correct because the curve isn't really like that. To put it another way as the curve starts to go over the knee non-lineary saturating it's not like it can be 'a bit of the integral'. Do you understand my confusion?

Not really , seems you're mixing cause and effect again because you leap right past necessary thought steps.

To illustrate the example, picture the magnetising current wave form distorting from a sinusoid to one with steeper peaks, or the flux sinusoid with shallower peaks, like it's flattening off. The derivative action is still there, just not 'fully'.

Derivative action is NOT there between flux and current.
relative permeability μ is not constant. so flux vs amps is not a simple y=mx+b but a quadratic of some sort.

time isn't even on that BH curve (ΦH in this case) .. right half is flux(independent variable, looks like sin of something) and mmf(dependent variable, amps) necessary to push that much Φ around the core

 

[tim9000]

Interesting, hopefully I can supply a higher callibar response this time. Now I have a bit more time I'll use some pictures, which I'd have like to have done before.

BH curve relates flux to mmf and mmf is ampsXturns. No derivative involved.
Have you forgot that Φ = μ X μ0 X N X I X A /length of path ? See any derivatives in that ?

Derivative action is NOT there between flux and current.
relative permeability μ is not constant. so flux vs amps is not a simple y=mx+b but a quadratic of some sort.

time isn't even on that BH curve (ΦH in this case) .. right half is flux(independent variable, looks like sin of something) and mmf(dependent variable, amps) necessary to push that much Φ around the core

I mean the relation between flux and voltage (although the primary and secondary currents would be in phase with voltage) being affected by the BH curve, thanks for reminding me about the flux actually is on the BH, that is a helpful perspective.
I see in your picture that the flux isn't a perfect sinusoid, rather that it has the shape of the BH curve. Say you were supplying a perfect sineusoidal voltage: So am I to take it that in a typical ferris core, the flux won't perfectly be the integral of the voltage sinusoid? Instead that it'll be sharper or blunter, depending on how far the flux peaks up the BH curve? Here I've drawn a picture of what I intened to illustrate the flux always has the same shape as the BH curve, just how much of it depends on the excitation V:
a small V, on the left only runs up the curve a bit, than runs down it again, in the middle is like you're picture, and on the right is like it's saturated. (excuse the crudeness in magnitudes etc)

I suppose that the ramifications of this are that the flux can never be of a greater rate of change than the input voltage, and that only in an infinitely permeable core would the flux be an exact sineusoid? Although one thing that has troubled me is that in your picture it looks as if the initail rate of change of the flux is actually greater than the initial rate of change of a sinusoid, but I'm putting this down to my imagination.Thanks for your perspective, you never disappoint.

 

[jim hardy]

(although the primary and secondary currents would be in phase with voltage)

have you thought that statement through?

Say you were supplying a perfect sineusoidal voltage: So am I to take it that in a typical ferris core, the flux won't perfectly be the integral of the voltage sinusoid?

A perfect sine voltage to an inductor with no winding resistance but a real core , is that your postulate?
What does Faraday say about voltage and flux?
Is that derivative/integral relation not just a property of the universe where we live? Do you also question Newton's assertion that F_ORCE = M_ASS X derivative of velocity ?

I see in your picture that the flux isn't a perfect sinusoid,

no it doesn't look that way to me either

rather that it has the shape of the BH curve.

more precisely, "rather its shape is determined by the BH curve " ?
The shapes of the BH and flux curves don't look at all similar to me.
The right half of this

is a graphical solution for current required to produce that red flux trace, which happens to resemble a sine function,
though i suppose you also could consider it red flux resulting from application of black currents Ob, Od, Of and Oh.
Only the first quadrant has significance, the other three are repeats by symmetry.

Say you were supplying a perfect sineusoidal voltage: So am I to take it that in a typical ferris core, the flux won't perfectly be the integral of the voltage sinusoid? Instead that it'll be sharper or blunter, depending on how far the flux peaks up the BH curve?

Not at all. Induced voltage and flux must have that derivative-integral relation.
Current is what distorts not flux. E=Ldi/dt and L is not constant with current because relative permeability is not constant.

no no no voltage is always slope(derivative) of flux and you have least voltage aligned with greatest slope

You seem determined to cast out all your prior knowledge and replace it with smooth sounding words.
Lavoisier addressed that tendency in human nature,

The method, too, by which we conduct our reasonings is as absurd; we abuse words which we do not understand, recollect, in your case

The only method of preventing such errors from taking place, and of correcting them when formed, is to restrain and simplify our reasoning as much as possible. This depends entirely upon ourselves, and the neglect of it is the only source of our mistakes. We must trust to nothing but facts: These are presented to us by Nature, and cannot deceive. We ought, in every instance, to submit our reasoning to the test of experiment, and never to search for truth but by the natural road of experiment and observation. Thus mathematicians obtain the solution of a problem by the mere arrangement of data, and by reducing their reasoning to such simple steps, to conclusions so very obvious, as never to lose sight of the evidence which guides them.

http://web.lemoyne.edu/~giunta/ea/lavprefann.html

 

[tim9000]

have you thought that statement through?

Perhaps not, though I thought I was drawing off prior knowlege. The preconception I had was that (forget the primary: bc has PF) that if there is just a resistive load on the secondary than the current will be in phase with the voltage

A perfect sine voltage to an inductor with no winding resistance but a real core , is that your postulate?

Thanks or the refinement, yes indeed it is.

What does Faraday say about voltage and flux?

That flux is (proportional to) the integral of voltage.

Is that derivative/integral relation not just a property of the universe where we live? Do you also question Newton's assertion that F_ORCE = M_ASS X derivative of velocity ?

Ha, well no because that is how force is defined to be. I expect it is a property of the universe we live in and I'm happy to take it on face value for now, especially because it's getting off my examination of a ferris core. But I still think 'the faster the flux chances, the more voltage induced' is a phenominan strange enough to contemplate in future, I'm sure there's another layer of explanation below. Point taken though.

no it doesn't look that way to me either

So what I'm getting at is 'does it want to be a sin wave?' but you're saying it's just a happy coincidence.

more precisely, "rather its shape is determined by the BH curve " ?
The shapes of the BH and flux curves don't look at all similar to me.
The right half of this

is a graphical solution for current required to produce that red flux trace, which happens to resemble a sine function,
though i suppose you also could consider it red flux resulting from application of black currents Ob, Od, Of and Oh.
Only the first quadrant has significance, the other three are repeats by symmetry.

I did notice that quadrant symmetry. Just to reitterate, that picture I drew, all that was happening to the flux wsa it had the shape of running up the BH curve to a different point (then the symmetry was repeated) that was the intended shape. Was that incorrect?

Not at all. Induced voltage and flux must have that derivative-integral relation.
Current is what distorts not flux. E=Ldi/dt and L is not constant with current because relative permeability is not constant.

View attachment 85862

no no no voltage is always slope(derivative) of flux and you have least voltage aligned with greatest slope

You seem determined to cast out all your prior knowledge and replace it with smooth sounding words.
Lavoisier addressed that tendency in human nature,

See I was thinking that the changing relative permeability modified the flux's integral/derivative relationship, but:
If it is current that distorts and not flux, why is the flux of the shape of a BH curve, and not the integral of the sinusoidal voltage?

I don't mean to be casting asside my knowledge I'm just feeling like the information of what is distorting and why is conflicted.
Could you elaborte on "E=Ldi/dt and L is not constant with current because relative permeability is not constant." please?
Thanks...

 

[jim hardy]

okay, mea culpa, I've been cramming multiple thoughts per post, just what i accuse you of doing

jim hardy said: ↑
What does Faraday say about voltage and flux?
to which you replied
That flux is (proportional to) the integral of voltage.

Good.
Can we agree that Faraday says
E = n dΦ/dt
and
∫Edt = n∫dΦ , which means Φ = ∫ voltage ?

so voltage and flux are related by an integral or differential relationship?

 

[tim9000]

okay, mea culpa, I've been cramming multiple thoughts per post, just what i accuse you of doing
Good.
Can we agree that Faraday says
E = n dΦ/dt
and
∫Edt = n∫dΦ , which means Φ = ∫ voltage ?

so voltage and flux are related by an integral or differential relationship?

Ha Ha, that's alright I'm making a near 5 hr railway trip today so I've got the time but concentration is hard. I just thought you were being a bit sarcastic ;P
'Rate of Change in flux is voltage, and flux is the area under the voltage function'

Yeah, Could you elaborte on "E=Ldi/dt and L is not constant with current because relative permeability is not constant." please, and how it's the "current" that distorts, not the flux? Because I'd consider the fact that the flux has the shape of the BH curve, instead of a nicer sine wave, a flux shape distortion, personally.
I'm still not convinced my scribblings were wrong, I know they look terrible though, but what I was trying to depict was the flux would run up the BH curve, how far depended on the magitude of the sine voltage excitation. By nature of the of the shape of the BH curve
I still don't unerstand why the flux has the BH shape (I know permeability won't let it in reality) if the maths (integral) says that is should be of a sineusoidal shape if the sinusoidal voltage (90deg lag), that's what I was saying earlier: it's like it wants to be a sinusoidal shape, but it can't.
Back to my postulate:

A perfect sine voltage to an inductor with no winding resistance but a real core , is that your postulate?

under that circumstance would the flux be an exact sinusoid?

Thanks Jim

 

[The Electrician]

See I was thinking that the changing relative permeability modified the flux's integral/derivative relationship, but:
If it is current that distorts and not flux, why is the flux of the shape of a BH curve, and not the integral of the sinusoidal voltage?

I think you're making some assumptions here. The red curve looks like it might be a sinusoid, which it should be if the applied voltage were a sinusoid. But, I don't think Jim intended it to be a sinusoid. You see it as a distorted sinusoid and this has led you to think that the flux might not really be the integral of the voltage.

Let me offer a somewhat different way of looking at the situation.

Consider a 10 ohm resistor. Suppose you apply 10 volts DC to that resistor. A current of 1 amp will flow through the resistor. Suppose you wanted 2 amps to flow through the resistor with 10 volts applied. How could you make this happen? You can't. A powerful way to think about a resistor is to realize that it's a two terminal device which imposes a relationship on the voltage across and current through it. You can't have current and voltage be independent in the resistor.

Similarly, the core in an inductor (and transformer) enforces a relationship between B and H. You can apply a current or a voltage, but whichever one you apply, the other is determined by the core; it cannot be just anything--it is constrained by the core.

So, if you apply a sinusoidal voltage to the winding of an iron cored inductor, the flux is proportional to the integral of the applied voltage, always, no exceptions. Since the integral of a sinusoidal wave shape is another sinusoidal wave, the flux will be sinusoidal also (assuming the resistance of the winding is negligible, which it usually is). What will the current be? It will be whatever is needed to provide the mmf (B) so that the intersection of B and H will be on the B-H curve of the iron core; the laws of physics require it.

Now, if another winding is placed on the core (a transformer now), the constraint imposed by the core is a constraint on the total mmf provided by all the windings.

With an unloaded secondary there will be no current in the secondary; the only mmf the core sees is the primary magnetizing current. Now, suppose we place a resistive load on the secondary. A current will flow which will oppose the primary excitation, reducing the flux in the core. This will lead to less winding voltage due to dΦ/dt opposing the applied voltage, which will lead to increased primary current. To bring things back to equilibrium the primary current must increase so that the total ampere-turns (mmf) applied to the core is determined by the flux applied to the B-H curve. In other words, the primary current increases until its mmf (essentially) cancels the mmf due to the secondary current, so that the effective mmf seen by the core is just the same as that due to the magnetizing current; that mmf is what is required by the flux and the B-H curve.

 

[jim hardy]

Thank you Electrician, clearly my approach has lacked something.

Ha Ha, that's alright I'm making a near 5 hr railway trip today so I've got the time but concentration is hard. I just thought you were being a bit sarcastic ;P

Sorry for coming across as, well, cross. I'm a plodder who needs to go one step at a time and it's frustrating being unable to keep up with folks who are more adroit .
I sure don't intend to hurt any feelings. I was trained by an old guard mentor who taught me that we have to holler and wave hands and exaggerate and sometimes even exchange insults to communicate effectively. Words alone are usually insufficient. He was a genuine "Secondhand Lion".

I've said before i appreciate that you question so, it shows real desire to understand at the gut (intuitive) level.

Rate of Change in flux is voltage, and flux is the area under the voltage function'

Good. Faraday and Maxwell gave us that and I'm not one to argue with them.
That's not limited to sine waves, is it?

That's my one thought for this post.

 

[The Electrician]

So, if you apply a sinusoidal voltage to the winding of an iron cored inductor, the flux is proportional to the integral of the applied voltage, always, no exceptions. Since the integral of a sinusoidal wave shape is another sinusoidal wave, the flux will be sinusoidal also (assuming the resistance of the winding is negligible, which it usually is). What will the current be? It will be whatever is needed to provide the mmf (B) so that the intersection of B and H will be on the B-H curve of the iron core; the laws of physics require it.

I made a typo in this post but the forum won't let me go back and edit it. Herewith the correction (a single letter) in red:

"It will be whatever is needed to provide the mmf (H) so that the intersection of B and H will be on the B-H curve of the iron core; the laws of physics require it."

I should also mention that the law of conservation of energy must be satisfied by the currents in primary and secondary, when there is a load on the secondary. If the secondary is delivering a current to a load, that represents energy delivered to the load. That energy has to come from the primary, so the primary current must increase to supply the energy that flows to the secondary load.

This energy explanation is correct, but doesn't really explain as much detail about what happens due to the presence of the core.

 

[jim hardy]

My one thought for this post is

Faraday's law makes no mention of MMF, H. It only involves flux Φ (or B X area) , voltage, and time.
B-H curve drags in the unrelated term MMF and omits time.
So how is a B-H curve relevant to Faraday's relation between volts and flux?

 

[jim hardy]

"It will be whatever is needed to provide the mmf (H) so that the intersection of B and H will be on the B-H curve of the iron core; the laws of physics require it."

Electrician is already there.
B-H curve relates flux to amps not to volts or time.
We need to grasp that, first for DC(no time function involved) then for AC where everything is affected by time.
One step at a time. Took me years but I'm slow.

 

[jim hardy]

Back to my postulate:

A perfect sine voltage to an inductor with no winding resistance but a real core ,...

under that circumstance would the flux be an exact sinusoid?

Sure !

e = -n*dΦ/dt Faraday's law
let e = Vsin(ωt)
Vsin(ωt) = -n*dΦ/dt
dΦ = -1/n * V dt
∫dΦ = -V/n * ∫sin(ωt dt

Φ= -V/n * (1/ω) * (-cos(ωt) ) + C_{onstant of integration}
observe negative signs cancel which is trig identity and Faraday's law agreeing
constant of integration is for initial condition
Φ = V/n * 1/ω * cos(ωt)
so flux is a cosine wave of amplitude (Volts per turn / ω)
which is your pure sinusoid..

Remember ages ago we said volts per turn is a measure of flux so long as we're talking sine waves at fixed frequency?

If you wish, set V=1 volt , number of turns =1, and ω=1 radian per second
then
e= sin(t)
Φ = cos(t)

we haven't introduced current yet.

that's my one thought f or this post. I hope my trig identities were right.

old jim

 

[jim hardy]

Yeah, Could you elaborte on "E=Ldi/dt and L is not constant with current because relative permeability is not constant." please, and how it's the "current" that distorts, not the flux?

yes. After we look at BH curve. Probably you've figured it out already.

 

[jim hardy]

from http://mumetal.co.uk/?p=110

Flux(dependent) versus MMF(independent).

No voltage, no time , no sine, no derivative.

It would be interesting to know how they measured flux at DC.
I've heard it can be done by connecting a good integrator to a winding on the core under study.
That of course gives a voltage proportional to flux. One could have real fun with a current output function generator , integrator and oscilloscope .

Back later.

old jim

 

[jim hardy]

nice little writeup on how they do it with AC

http://www.eleceng.adelaide.edu.au/personal/wlsoong/documents/pebn005BHcurveandironlossmeasurementsformagneticmaterials.pdf

they too use a coil for flux detector

and a DSP method of integration that i don't understand. .

That trick is too new for this old dog

 

[thankz]

I'm waiting till theirs no more responses to this thread to save it, old jim you have done an excellent job I must say, keep up the good work.

edit: do you know what the lambda sign in the equation stands for?

 

[jim hardy]

I'm waiting till theirs no more responses to this thread to save it, old jim you have done an excellent job I must say, keep up the good work.

edit: do you know what the lambda sign in the equation stands for?

What ? I'm really despondent about it , feeling i botched things up.

I want to talk through the BH curve but i do better in the mornings. Getting old.

A bigger snip from that link says λ is flux .

It has to be just the output of whatever integrator you connect to sense winding.

Observe in their formula B(t) = (two constants) X λ(t) , and we know flux is integral of induced voltage,,,
and look at their formula... ∫V_sensedt and λ_sense are interchangeable

I'd use an analog integrator and oscilloscope.
I have done that but when i did i was using sine waves where all you see is phase shifted sinewaves .
The core i had was so eddy-current ridden that nothing made sense at the time, voltage and flux weren't 90 degrees out like an integral should be, also current and flux weren't in phase. ...
So i switched to those triangle waves posted way back... then i understood. My applied current wasn't the only current flowing - eddy currents delay magnetization, opposing it per Lenz. My core was a solid bar not laminated so eddy currents ran rampant. They cancel flux making the iron appear not only lossy but less permeable.
So it's important to get the basics down pat using ideal parts then correct back to reality.
That's why right now I'm sticking with pure sine wave voltage.
After we do that we can look instead at pure sine wave current

and hopefully we'll have a jedi master in Tim. Bless his patient heart...

Thanks for the kind words - helps an old guy feel less useless.

jh

 

[tim9000]

I'm still up to post #45, I intend to catch up this weekend, looking forward to it!

 

[jim hardy]

Been trying to figure out what path to take with BH.

Splattering equations doesn't work for me, i have to plod through mechanics and then the formulas appear natural.

Thanks - i'll get next step up real soon.

Been trying to paste mirror image of that mu-metal BH to make it symmetric about zero.

Then sweep current, that's straightforward..
Then sweep flux , which will point up nonlinearity of current to flux in iron (unlike free space)
both for DC

then for sine?

old jim

 

[tim9000]

Preliminary post: (I need to re-read everything again)

Consider a 10 ohm resistor. Suppose you apply 10 volts DC to that resistor. A current of 1 amp will flow through the resistor. Suppose you wanted 2 amps to flow through the resistor with 10 volts applied. How could you make this happen? You can't. A powerful way to think about a resistor is to realize that it's a two terminal device which imposes a relationship on the voltage across and current through it. You can't have current and voltage be independent in the resistor.

That post was a joy to read to make the analogy for the B and H in the core.

Similarly, the core in an inductor (and transformer) enforces a relationship between B and H. You can apply a current or a voltage, but whichever one you apply, the other is determined by the core; it cannot be just anything--it is constrained by the core.

H'mm, ok, I sort of need to ask another question here, which is about making the curve. So is it that you measure the voltage applied to the OC core to get the proportion of flux density B, and you measure the OC current (mag current) to get the proportion of H? (so B is related to voltage through area, and an integration; and H is related to current through turns number?) Because when taking those measurements, assuming what I said is correct, I'm not sure how to then create the exact 'B-H' curve.
Edit: ah so you can either have a "Flux(dependent) versus MMF(independent)" or mmf dependant flux independant measurement to get the B-H curve? Because what I just said was you read the volt meter, record current and voltage, increase current by an interval, take another reading. But if you were to have "Flux(dependent) versus MMF(independent)" you'd read the current, and voltage, then increase the current an interval and repeat? So if you were to do it this way, you'd just be recording the magnitude of the voltage and it is differentiated, it just doesn't matter because you don't notice the phase difference.

I should also mention that the law of conservation of energy must be satisfied by the currents in primary and secondary, when there is a load on the secondary. If the secondary is delivering a current to a load, that represents energy delivered to the load. That energy has to come from the primary, so the primary current must increase to supply the energy that flows to the secondary load.

This energy explanation is correct, but doesn't really explain as much detail about what happens due to the presence of the core.

It is good to keep that in mind, yes I think Jim and I fleshed out pretty well how the energy is transferred from Primary to Secondary through the ideal transormer in the real transformer model. (i.e not through 'inductance')

Faraday's law makes no mention of MMF, H. It only involves flux Φ (or B X area) , voltage, and time.
B-H curve drags in the unrelated term MMF and omits time.
So how is a B-H curve relevant to Faraday's relation between volts and flux?

Very interesting point! Yes! that's an excellent question! I couldn't contextualise the problem, so how is the B-H cure relevant to Faraday? ->

B-H curve relates flux to amps not to volts or time.
We need to grasp that, first for DC(no time function involved) then for AC where everything is affected by time.
One step at a time.

So are you (both) saying it's not relevant at all? That infact one is applicable when there is DC measurement and the other when there is AC measurement/opperation taking place?

nice little writeup on how they do it with AC

http://www.eleceng.adelaide.edu.au/personal/wlsoong/documents/pebn005BHcurveandironlossmeasurementsformagneticmaterials.pdf

they too use a coil for flux detector

Hmm, I'll have to have a read of that later.So I have to remember, there isn't just saturation that will change the shape of the flux function (from constant Amp and freq input) but also eddy currents that delay phase and reduce amplitude.

I need to get some varification on what I've said thus far; I'm a bit confused thinking about DC in the context of a magnetic core because I always use AC, so when I used the term DC I just think it's like using AC but not caring about 'time'.
A bit of a re-cap, I don't want to mix mutually exclusive dependant variables so I say this at that peril. I understand that out of current and voltage only one can be defined at a time. Say we have an open circuit transformer (or inductor) and the voltage is independant commodity. The current drawn (mag current) will be the necessary amount to yield the required H for the flux density (B) produced by (faraday's) the voltage excitation. As the voltage magnitude is increased the necessary current has to start to spike up as the core saturates. But to me this sounds like the flux should still be a nice sineusoid (from B) even while the core is starting to saturate. (contrary to pictures I've seen of the flux flattening out) So the flux would flatten out sort of only if you were using the primary (or mag ) current as the indepenant quantity?

I'm greatful for all the attention and effort this thread has recieved, particularly for Jim keeping me on a stepwise thinking track.

 

[The Electrician]

H'mm, ok, I sort of need to ask another question here, which is about making the curve. So is it that you measure the voltage applied to the OC core to get the proportion of flux density B, and you measure the OC current (mag current) to get the proportion of H? (so B is related to voltage through area, and an integration; and H is related to current through turns number?) Because when taking those measurements, assuming what I said is correct, I'm not sure how to then create the exact 'B-H' curve.
Edit: ah so you can either have a "Flux(dependent) versus MMF(independent)" or mmf dependant flux independant measurement to get the B-H curve? Because what I just said was you read the volt meter, record current and voltage, increase current by an interval, take another reading. But if you were to have "Flux(dependent) versus MMF(independent)" you'd read the current, and voltage, then increase the current an interval and repeat? So if you were to do it this way, you'd just be recording the magnitude of the voltage and it is differentiated, it just doesn't matter because you don't notice the phase difference.

So I have to remember, there isn't just saturation that will change the shape of the flux function (from constant Amp and freq input) but also eddy currents that delay phase and reduce amplitude.

I need to get some varification on what I've said thus far; I'm a bit confused thinking about DC in the context of a magnetic core because I always use AC, so when I used the term DC I just think it's like using AC but not caring about 'time'.
A bit of a re-cap, I don't want to mix mutually exclusive dependant variables so I say this at that peril. I understand that out of current and voltage only one can be defined at a time. Say we have an open circuit transformer (or inductor) and the voltage is independant commodity. The current drawn (mag current) will be the necessary amount to yield the required H for the flux density (B) produced by (faraday's) the voltage excitation. As the voltage magnitude is increased the necessary current has to start to spike up as the core saturates. But to me this sounds like the flux should still be a nice sineusoid (from B) even while the core is starting to saturate. (contrary to pictures I've seen of the flux flattening out) So the flux would flatten out sort of only if you were using the primary (or mag ) current as the indepenant quantity?

I'm greatful for all the attention and effort this thread has recieved, particularly for Jim keeping me on a stepwise thinking track.

The B/H curve is only used where DC is concerned. The way it is measured is to apply a current and measure the flux with a flux meter. A more modern method which I have used (because flux meters are not a common instrument) is to use a Hall effect device (https://en.wikipedia.org/wiki/Hall_effect) to measure the flux. A DC current is applied, and the flux is measured and plotted for enough points to get a good curve.

But, when AC is used, the B/H curve opens up into a loop because of eddy current and hysteresis losses. The values of B and H are constrained to lie on this loop, and the time variable comes into play. See this thread (http://forum.allaboutcircuits.com/threads/confused-about-transformer-saturation.37358/page-2) starting at post #23 and following for an example of measuring the hysteresis loop for an iron core.

If a sinusoid of voltage is applied to a winding on a core, the flux will be sinusoidal even when the core is well into saturation, provided the resistance of the wire making up the winding is zero. If the winding resistance is not zero, then the voltage seen by the core will be reduced by the I*R voltage drop in the winding due to the current drawn through that winding's resistance. If the core is saturating, the peaky current will cause the voltage seen by the core to not be sinusoidal, and, of course, the integral of that non-sinusoidal voltage will not be a sinusoid either; this is where reality differs from theoretical perfection.

 

[jim hardy]

Wow !
What a delight to see there's still interest in this thread - i was afraid i'd beaten the proverbial horse to death..

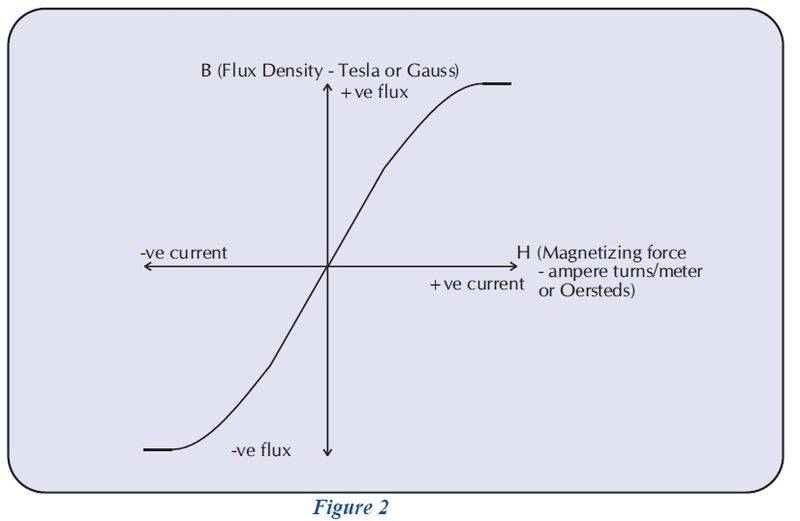
I picked this curve because of the units they used.

I wanted to proceed one thought per post
so here goes.

It's a DC curve. That's the place to start developing thought process.
http://mumetal.co.uk/?p=110

Mu metal is very permeable, used for magnetic shielding.

Horizontal unit on graph is amp per meter,
which is same as amp-turns per meter,
so we can take the small mental leap that it's amps through some particular winding on some particular core of this particular alloy,
made to the specific dimensions such that one amp gives one amp-turn per meter.
That keeps the arithmetic simple. I need that.

let me add to that graph a couple lines representing one thought:
(pardon my awkwardness with Paint)

Let us consider current our independent (controlled) variable.
I apply ten amps and get what, 1.04 Tesla ?
I apply eight amps and get 1.0 Tesla?
Thirty amps gives just over 1.1 Tesla?
Sixty amps gives maybe 1.18 Tesla?

It's nonlinear as we all know.
That's because the domains in the iron align, but there's only so many of them.
Hyperphysics link (Thanks dlgoff)
http://hyperphysics.phy-astr.gsu.edu/hbase/solids/ferro.html

Now
if Inductance is flux linkages per ampere,
which is flux per amp-turn,
is it apparent that for our mu-metal core
inductance would calculate out to a function of current?

amps ...flux ... inductance
8 ... 1 ... 1/8 = 0.125
10 ... 1.04 ... .. 1.04/10 = 0.104
30 ... ~1.1 ... 1.1/30 = 0.037
60 .. 1.18 .. ... 1.18/60 = 0.02
a six to one turndown.
And that's why we operate most inductors below the knee, where our approximation of constant μ_relative is close enough .

Observe out beyond 40 amps incremental permeability was 0.0015.
Dividing that by permeability of free space, 4ΠE-7 gives 1194 for μ way out there past saturation
no wonder they call it mumetal

Once we get comfortable with DC we're ready for AC.

Thanks to all who contribute - if my step by step plodding seems childish, well, i sure struggled with magnetics and had to work myself through this very thought process.

next we'll make flux the controlled variable and observe what that does to current. Still DC.

Let me know before the horse dies, will you ?

old jim