jim hardy
Science Advisor
Homework Helper
Dearly Missed
- 9,864
- 4,896
tim9000 said:P.S, These are the curves I plotted the other week, they are from the same E core, the one at the top is the centre leg, which was twice as thick as the outter legs, the bottom is one of the side legs. I think the steel might have been M4 grain oriented silicon steel, I measured it as 0.27mm thick. From my brief looking on the net I think the max relative permiability or affective relative permiability or whatever is 14, but I'm not sure, what do you reckon(?):
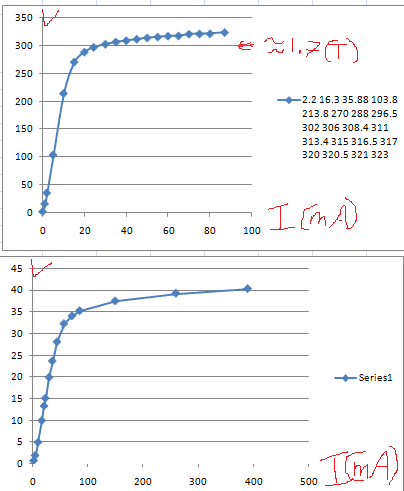
Thanks!
Are vertical scales really 10X different ? What are they -- volts ? millivolts per turn? Was this at line frequency ?
judging by shape of your curves It takes maybe 20 ma to saturate when driving center leg
more like 80 to saturate when driving an outside leg ?
When driving the Outside leg, it will saturate first because flux goes from it into the 3x greater area of the other two legs
so you have a core that's part saturated and mostly not saturated.
A picture or sketch of your setup would be informative.
How did you calculate effective permeability?
There's some error introduced by using AC meters to measure non-sinewave current after the knee. An oscilloscope would be really handy.