tim9000
- 866
- 17
Hi all,
I've been having a conversation with a brilliant PF memeber about power transfer, but I wouldn't be surprised if my inability for comprehension has driven them to their knees.
I don't quite remember/understand how the concept of power fits into a transformer. I used to think that it was something to do with inductance storing energy from the primary in the magnetic field, then it would go out through the secondary.
Basically I know there is stored magnetic energy in inductance in the core, but I've been told it has nothing to do with power transfer (and it's purely Faradays law).
First, I want to get someone to clarify this:
I assume the inductance from Xm, is that actually the mutual inductance from both primary and secondary coils, ignoring leakage inductance, what I was thinking was something like:
Average Energy in core = 1/2 *L*I2 = 1/2 * (Xm*jω) * (IO)2
=1/2 * L1*(I1)2+M*I1*I2+ 1/2 *L2*(I2)2
=1/2 * N1Φ12*I1+M*I1*I2+ 1/2 *N2Φ21*I2where 1 is primary, and 2 is secondary, LΦ12 is flux from primary without leakage, Φ21 is flux from secondary
and total core Φ = Φ12 - Φ21
Using the characteristic of:
So Thigns I'm seeking to confirm are:
Q1: (from the diagram) is the power of the TX going from one side to the other is equal to Ep*Is
= Es*Ip/a
This seems possible to me because I imagine that power is pretty much contingent on the secondary, as it's just an inductor when there is no secondary current. This should be true regardless?
Q2: Jim said that power goes straight across, without waiting (like a sinusoid) So is that average Energy equation that I wrote above right?
And if so, (given energy = power*time) does this mean:
Aveage Energy in core = 1/2 * (Xm*jω) * (IO)2
is going swishing and swoshing in and out of the core as reactive power?
So if Inductive energy has nothing to do with power transfer, then does one need to think of power being transferred through the ideal TX as:
At Case 1>OC sec: no power
At Case 2>small load on secondary, not much current through secondary: Es = N d(Φ12 - Φ21)/dt
At Case 3>large load on secondary, lots of secondary current: means lots of Φ21 pushing back, reduces the back EMF of Ep, means more current will flow through Ip, which will mean Ep*Is will increase and more flux will be produced for Φ12, which will mean that there is Es = N d(Φ12 - Φ21)/dt will increase as Is increase.
And, that's how the power is transferred across the Ideal TX?
I've been having a conversation with a brilliant PF memeber about power transfer, but I wouldn't be surprised if my inability for comprehension has driven them to their knees.
I don't quite remember/understand how the concept of power fits into a transformer. I used to think that it was something to do with inductance storing energy from the primary in the magnetic field, then it would go out through the secondary.
Basically I know there is stored magnetic energy in inductance in the core, but I've been told it has nothing to do with power transfer (and it's purely Faradays law).
First, I want to get someone to clarify this:
I assume the inductance from Xm, is that actually the mutual inductance from both primary and secondary coils, ignoring leakage inductance, what I was thinking was something like:
Average Energy in core = 1/2 *L*I2 = 1/2 * (Xm*jω) * (IO)2
=1/2 * L1*(I1)2+M*I1*I2+ 1/2 *L2*(I2)2
=1/2 * N1Φ12*I1+M*I1*I2+ 1/2 *N2Φ21*I2where 1 is primary, and 2 is secondary, LΦ12 is flux from primary without leakage, Φ21 is flux from secondary
and total core Φ = Φ12 - Φ21
Using the characteristic of:
Where the inductance is on the primary circuit, power goes in from source, and goes back out to the source. So that power waveform isn't what's going to a secondary load.jim hardy said: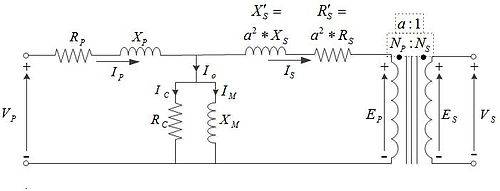
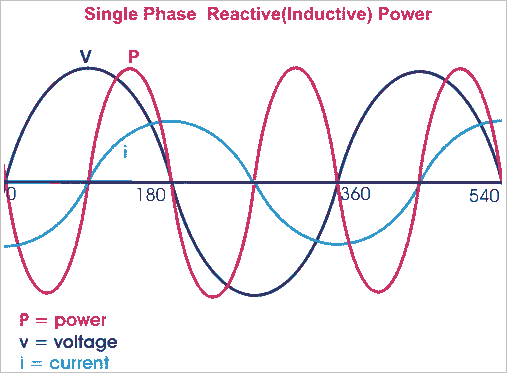
So Thigns I'm seeking to confirm are:
Q1: (from the diagram) is the power of the TX going from one side to the other is equal to Ep*Is
= Es*Ip/a
This seems possible to me because I imagine that power is pretty much contingent on the secondary, as it's just an inductor when there is no secondary current. This should be true regardless?
Q2: Jim said that power goes straight across, without waiting (like a sinusoid) So is that average Energy equation that I wrote above right?
And if so, (given energy = power*time) does this mean:
Aveage Energy in core = 1/2 * (Xm*jω) * (IO)2
is going swishing and swoshing in and out of the core as reactive power?
So if Inductive energy has nothing to do with power transfer, then does one need to think of power being transferred through the ideal TX as:
At Case 1>OC sec: no power
At Case 2>small load on secondary, not much current through secondary: Es = N d(Φ12 - Φ21)/dt
At Case 3>large load on secondary, lots of secondary current: means lots of Φ21 pushing back, reduces the back EMF of Ep, means more current will flow through Ip, which will mean Ep*Is will increase and more flux will be produced for Φ12, which will mean that there is Es = N d(Φ12 - Φ21)/dt will increase as Is increase.
And, that's how the power is transferred across the Ideal TX?
Last edited: