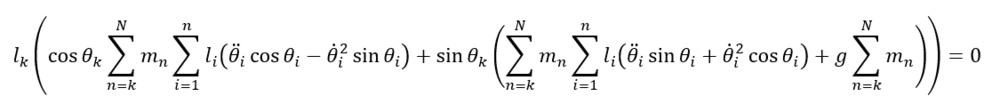In the configuration as attached sketch for 2D n-fold pendulum shows
(x_0,y_0)=(0,0)
(x_i,y_i)=(x_{i-1},y_{1-1})+(l_i \cos\theta_i, l_i \sin\theta_i)=(\sum_{j=1}^i l_j\cos\theta_j, \sum_{j=1}^i l_j\sin\theta_j)
(\dot{x_i},\dot{y_i})=(\sum_{j=1}^i l_j (-\sin\theta_j) \dot{\theta_j}, \sum_{j=1}^i l_j\cos\theta_j \dot{\theta_j})
Lagrangean of the system is
L=\sum_{i=1}^n \frac{m_i}{2}(\dot{x_i}^2+\dot{y_i}^2)+g\sum_{i=1}^n m_i x_i
with gravity force applying to x positive direction. Express L as ##L(\theta_1, \theta_2,...,\theta_n, \dot{\theta_1}, \dot{\theta_2}, ... , \dot{\theta_n})##
L=\sum_{i=1}^n \frac{m_i}{2}[\{\sum_{j=1}^i l_j (-\sin\theta_j) \dot{\theta_j}\}^2+\{\sum_{j=1}^i l_j \cos\theta_j\ \dot{\theta_j}\}^2]+g\sum_{i=1}^n m_i \sum_{j=1}^i l_j\cos\theta_j
We get equation of motion or Lagrangean equation from this Lagrangean, e.g.
\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_k}}=\frac{d}{dt}\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\sin\theta_j) \dot{\theta_j}\}l_k (-\sin\theta_k)+\{\sum_{j=k}^i l_j \cos\theta_j\ \dot{\theta_j}\}l_k \cos\theta_k]
=\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\cos\theta_j) \dot{\theta_j}^2\}l_k (-\sin\theta_k)+\{\sum_{j=k}^i l_j (-\sin\theta_j\ \dot{\theta_j}^2\}l_k \cos\theta_k]
+\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\sin\theta_j) \ddot{\theta_j}\}l_k (-\sin\theta_k)+\{\sum_{j=k}^i l_j \cos\theta_j\ \ddot{\theta_j}\}l_k \cos\theta_k]
+\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\sin\theta_j) \dot{\theta_j}\}l_k (-\cos\theta_k)\dot{\theta_k}+\{\sum_{j=k}^i l_j \cos\theta_j\ \dot{\theta_j}\}l_k(- \sin\theta_k) \dot{\theta_k}]
equals to
\frac{\partial L}{\partial \theta_k}=\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\sin\theta_j) \dot{\theta_j}\}l_k (-\cos\theta_k)\dot{\theta_k}+\{\sum_{j=k}^i l_j \cos\theta_j\ \dot{\theta_j}\}l_k (-\sin\theta_k)\dot{\theta_k}]+g\sum_{i=k}^n m_i \ l_k(-\sin\theta_k)
So the resulted equation is
\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\cos\theta_j) \dot{\theta_j}^2\} (-\sin\theta_k)+\{\sum_{j=k}^i l_j (-\sin\theta_j)\ \dot{\theta_j}^2\} \cos\theta_k<br />
+\{\sum_{j=k}^i l_j (-\sin\theta_j) \ddot{\theta_j}\} (-\sin\theta_k)+\{\sum_{j=k}^i l_j \cos\theta_j\ \ddot{\theta_j}\}\cos\theta_k<br />
-g (-\sin\theta_k) ]=0
or
\sum_{i=k}^n m_i[\ \sum_{j=k}^i l_j \sin(\theta_k-\theta_j) \dot{\theta_j}^2<br />
+\sum_{j=k}^i l_j \cos(\theta_k-\theta_j )\ddot{\theta_j} +g \sin\theta_k\ \ ]=0
where k=1,2,...,n. Coefficients of g have trigonometric function though formula OP does not have it.
These n equations give you formula of ##\ddot{\theta_k}## as functions of ##\theta_i##s and ##\dot{\theta_i}##s, which you are looking for.