How to calculate the torque of slider crank?

[Rachel_S]

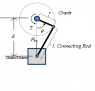
As shown in this picture, if Fb, l (length of connecting rod), r (radius of crank) and θ is given, how to calculate the torque the slider crank?
I know it can be a simple question for Mechanical Engineering majors, but I am an Electrical Engineering major and have very little knowledge in Mechanical Engineering. I am working on a project related to slider crank systems and really need to know this. It would be great if you could tell me which book introduces slider crank torque calculation too.
Thanks!

 

[tiny-tim]

Hi Rachel_S! Welcome to PF!

Torque = Fdsinθ, or F x d (same thing).

So calculating torque isn't really engineering, it's geometry.

You need a book on geometry, or on trigonometry, or maybe on the elements of vectors (particularly the cross product).

 

[nvn]

I know it can be a simple question for Mechanical Engineering majors ...

Rachel_S: No, it is not necessarily a simple question. You must work out the geometry, trigonometry, and algebra, to derive the answer. I currently obtained the following torque, as a function of theta.

T(θ) = [Fb/(L^2)]*(r*sin θ)*{ L^2 - (r*sin θ)^2 + (r*cos θ)*[L^2 - (r*sin θ)^2]^0.5 }​

Here is another way to obtain the same answer, using asin(). Let phi(θ) = asin[(r/L)*sin θ]. Then,

T(θ) = r x F = Fb*cos[phi(θ)]*r*sin[θ + phi(θ)].​

 

[JEP]

nvn - excellent & thorough solution & response. Not nearly as simple as one (1) would like to think! All trig & algebra and all that, however, real super easy to get all messed up somewhere.

Hey ... hope you can help here. We've got a very similar mechanism that we need to determine the applied thrust to overcome a known torque across some 120 degrees or so of crank rotation with an added twist. Our mechanism is an "Offset Slider-Crank Mechanism" instead of the more common "On Center (No Offset) Slider-Crank Mechanism" shown.

How does that affect the equations above?

If it matters, the slider will be offset to the right of the crank pivot AND offset far enough to allow the slider to pass over and beyond the crank pivot and continue to the "dead mans" position and then continue to travel to rotate the crank back fifteen (15) to thirty (30) degrees or so. L is something like 1-3/4 x r and offset is something like 1-1/4 times r if that helps any.

We've got the translational & rotational stuff all figured out in Excel & MatLAB, verified by AutoCAD layout. Pretty sweet actually ... two (2) solutions ... one (1) solving for slider stroke with given crank rotation, the second solving for crank rotation given slider stroke. So we already have any and all angles we could ever dream of, just can't quite get out of the "brain dead" mode to find the solution, especially don't know quite what to do with the offset.

Oh yeah, almost forgot. We're in real life here in real time here, so we'll need to consider friction of slider as well both knuckles (joints) ... not to be confused with this knucklehead!

Any thoughts around a similar solution to this? My poor little AND old pea brain is not getting this one done w/o asking for some help!

THANK YOU SO MUCH!