SUMMARY
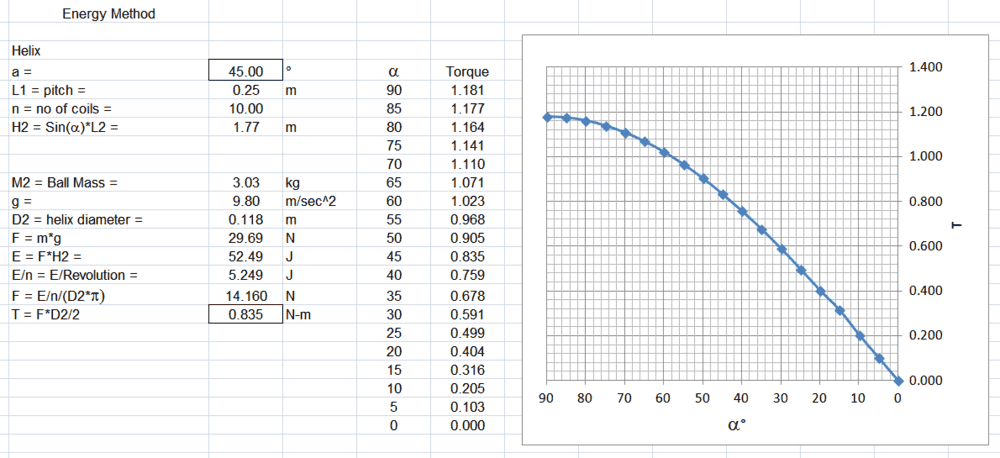
The discussion focuses on calculating the torque required for a steel ball to ascend a spiral tube at a uniform speed. Key parameters include the masses of the steel ball (M2), the spiral tube (M3), and the central shaft (M1), along with the gravitational force (g) and the friction coefficient (u). The torque can be calculated using the formula: F = (M1 + M2 + M3) * (D2 / 2) * u + M2 * g * sin(L / D) * sin(45°) * (D2 / 2 - s - r). The conversation also emphasizes the importance of understanding the geometry of the spiral and the forces acting on the ball.
PREREQUISITES
- Understanding of torque calculations in mechanical systems
- Familiarity with the principles of conservation of energy
- Knowledge of helical geometry and its applications
- Basic concepts of friction and its effects on motion
NEXT STEPS
- Research "Torque calculations for helical systems" to deepen understanding of the mechanics involved.
- Study "Conservation of energy in mechanical systems" for insights on energy transfer in motion.
- Explore "Friction coefficients in mechanical design" to understand how friction impacts performance.
- Investigate "Helical tube pump design" for practical applications of the discussed concepts.
USEFUL FOR
Mechanical engineers, physics students, and anyone involved in the design and analysis of systems utilizing helical structures or torque calculations.