SUMMARY
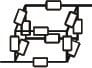
The discussion focuses on calculating the total resistance in a box-formation resistor network consisting of 12 equal resistors. The key equations utilized are the series resistance formula (R = r1 + r2 + ... + ri) and the parallel resistance formula (1/R = 1/r1 + 1/r2 + ... + 1/ri). The application of Kirchhoff's laws is emphasized for analyzing current distribution across nodes. The proposed method involves simplifying the network by treating groups of resistors in parallel, ultimately leading to a total resistance calculation.
PREREQUISITES
- Understanding of series and parallel resistor configurations
- Familiarity with Kirchhoff's laws
- Basic circuit analysis techniques
- Knowledge of voltage sources and current flow in circuits
NEXT STEPS
- Study advanced applications of Kirchhoff's laws in complex circuits
- Learn about equivalent resistance in more intricate resistor networks
- Explore simulation tools like LTspice for circuit analysis
- Investigate the impact of resistor values on total resistance in parallel and series combinations
USEFUL FOR
Electrical engineering students, circuit designers, and hobbyists interested in understanding resistor networks and circuit analysis techniques.