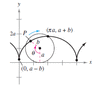How to Derive Parametric Equations for a Curtate Cycloid?

[iberhammer]

A wheel radius a rolls along a line without slipping. The curve traced by a point P that is b units from the center (b < a) is called a curtate cycloid (see figure). Use the angle θ to find a set of parametric equations for this curve.




I went through the book, went to the math lab at my university, and still I cannot find the right solution. I had

x=a(θ-sinθ)
y=a(1-cosθ)

but my tutor just said to replace a and b. I tried that on webassign and still, I received a red mark wrong! I could use some help if anyone could spare any? Thank you all

 

[LCKurtz]

Of course, your answer can't be correct because it doesn't involve b.

Try thinking of the position vector of the moving point of radius b as the sum of two vectors. The first is the vector from the origin to the center of the circle. The x and y components of that vector only involve a. Then think of the vector from the center of the circle of radius b and angle theta. Write its components in terms of b and theta. Then add the two vectors up.