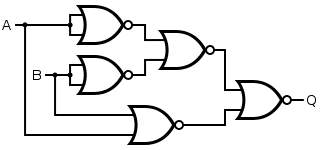
SUMMARY
This discussion details the derivation of a XOR gate using only NOR gates. The key transformation involves manipulating the logical expressions for XOR (AB' + A'B) and NOR (A'B') to create a circuit equivalent to a 2-input XOR. The final formula derived is a combination of NOR operations that effectively constructs the desired XOR functionality. The process utilizes fundamental Boolean algebra to achieve the conversion from NOR to XOR.
PREREQUISITES
- Understanding of Boolean algebra
- Familiarity with NOR gate logic
- Knowledge of circuit design principles
- Experience with LogiSim or similar circuit simulation tools
NEXT STEPS
- Study the derivation of XOR using NAND gates for comparison
- Explore advanced Boolean algebra techniques
- Learn about circuit simplification methods
- Experiment with LogiSim to build and test the derived XOR circuit
USEFUL FOR
This discussion is beneficial for electrical engineers, computer scientists, and hobbyists interested in digital logic design and circuit optimization using basic logic gates.