SUMMARY
This discussion focuses on finding integrals of parent functions without any horizontal or vertical shifts, specifically using the function form Cxp where p ≠ -1. The integral can be computed using the formula Cxp+1/(p+1). A significant challenge arises when approximating values like 9^{1/7} and 14^{8/7} using a basic calculator limited to addition, subtraction, multiplication, and division. Participants suggest methods such as polynomial expansion and iterative approaches to achieve adequate approximations.
PREREQUISITES
- Understanding of integral calculus and parent functions
- Familiarity with polynomial expansion techniques
- Basic knowledge of numerical approximation methods
- Proficiency in using calculators for basic arithmetic operations
NEXT STEPS
- Research polynomial expansion methods for approximating functions
- Learn about numerical methods for calculating roots, such as the Newton-Raphson method
- Explore integral calculus techniques for functions without shifts
- Study iterative approximation techniques for complex calculations
USEFUL FOR
Students and educators in mathematics, particularly those focusing on calculus, as well as anyone interested in numerical methods for function approximation.
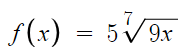
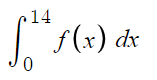with a calculator that can only add, subtract, multiply, divide