- #1
woaname
- 40
- 0
Homework Statement
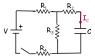
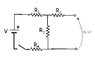
i tried using the usual Q=VC to answer this question for a multiloop RC circuit, "What is Q(∞), the charge on the capacitor after the switch has been closed for a very long time?" and my answer was wrong. clearly, i can't find Qmax because the resistors contribute to the voltage drop.
i can't seep to wrap my head around finding the proper equations for finding Q using kirchhoffs laws and end up having multiples unknowns. the image of the schematic is attached. any help? thnx.
Homework Equations
kirchoff's loop rule and junction rules
I) I1=I2+I3
II) -I2R2+Q/C+I3R3=0
III) -I3R3-I4R4+V-I1R1=0
The Attempt at a Solution
based on a previous question, i was able to find I4= V ((Req for R2andR3)+R4+R1)
Attachments
Last edited: