How to Find the First Buckling Load from the Deflection Equation?

[Master1022]

Homework Statement

Use the derived deflection equation to calculate the first buckling load?

Relevant Equations

Derived equation

Hi,

I was working through a problem about calculating buckling loads. The problem had the following geometry (I apologise for the poor drawing skills):

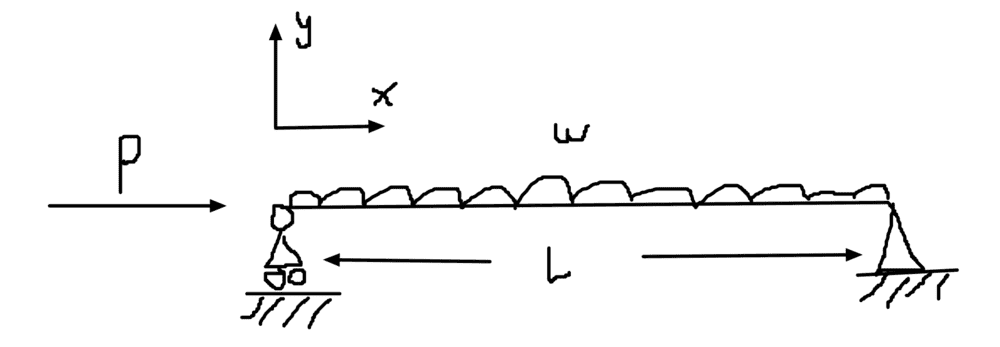and the total length is $L$.

The boundary conditions are therefore:
1. $y(0) = 0$
2. $y(L) = 0$

My approach:
After taking a cut and taking moments we can eventually get the following solution (which agrees with the answer):

$$ y(x) = \frac{-wEI}{P^2} cos(\beta x) + \frac{wEI}{P^2} \left(\frac{cos(\beta L) - 1}{sin(\beta L)} \right) sin(\beta x) - \frac{w}{2P} x^2 + \frac{wL}{2P}x + \frac{wEI}{P^2} $$

where $\beta^2 = \frac{P}{EI}$

but I really have no clue how to proceed by using this equation to find the first buckling load. Usually we find expressions for $\beta$ that arise from the boundary conditions...

Any help is greatly appreciated. Thanks

 

[Lnewqban]

We could consider this case as a buckling column, axially loaded by P and laterally loaded by a uniformly distributed load W.
Note that the column is pivoted in both ends, which, together with the lateral load, reduces the magnitude of critical P.

This Math is too complicated for me, but it may help you:
https://www.continuummechanics.org/multiloadcolumnbuckling.html

 

[Master1022]

We could consider this case as a buckling column, axially loaded by P and laterally loaded by a uniformly distributed load W.
Note that the column is pivoted in both ends, which, together with the lateral load, reduces the magnitude of critical P.

This Math is too complicated for me, but it may help you:
https://www.continuummechanics.org/multiloadcolumnbuckling.html

Thank you very much for sharing this @Lnewqban - I will try to make my way through this!

Although, I feel that this method, whilst correct, might slightly be a bit too long for 2 marks of working. I have managed to get a hint from the professor that perhaps we can use the displacement at $x = L/2$ but I don't really see how that information is useful. Are you able to see how that could be useful?

In the meanwhile, I will read through that link.

 

[sully_01]

Your professors hint is correct. The first buckling mode is likely to be when the maximum deflection occurs at the centre of the beam. Hence dy/dx evaluated at x = L/2 will be 0, and you can solve for the corresponding Beta. (The math simplifies down quite a bit and you'll end up having to solve a simple trigonometric equation!).