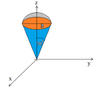
SUMMARY
The volume of a hemisphere on top of a cone can be calculated using triple integrals in spherical coordinates. The integral setup involves the limits for radius \( r \) from 0 to \( (r + R) \cos \theta \), with \( \theta \) ranging from 0 to \( \frac{\pi}{6} \) and \( \phi \) from 0 to \( 2\pi \). The integral simplifies to \( 2\pi \int \frac{1}{3} \left[ ((r+R) \cos \theta)^3 - r^3 \right] \sin \theta \, d\theta \). The final radius \( R \) is crucial for determining the volume, and the problem requires careful attention to the geometry of the cone and hemisphere.
PREREQUISITES
- Understanding of triple integrals in spherical coordinates
- Knowledge of volume calculation for geometric shapes
- Familiarity with the properties of integrals and trigonometric functions
- Basic concepts of calculus, particularly integration techniques
NEXT STEPS
- Study the application of triple integrals in spherical coordinates
- Learn about the volume of cones and how to integrate them with other shapes
- Explore advanced integration techniques for complex geometric problems
- Investigate the relationship between angles and volumes in conical shapes
USEFUL FOR
Students and professionals in mathematics, particularly those focused on calculus and geometric analysis, as well as anyone tackling problems involving volumes of composite shapes like cones and hemispheres.