How to implement a transfer function in Simulink with variable coefficients?

[MoonDiver]

Homework Statement

Implement in Simulink two filters using transfer functions with variable coefficients and passing a gaussian noise. The two filters are:

Relevant Equations

F(s) = ((5d)^(1/2))/(b+s);
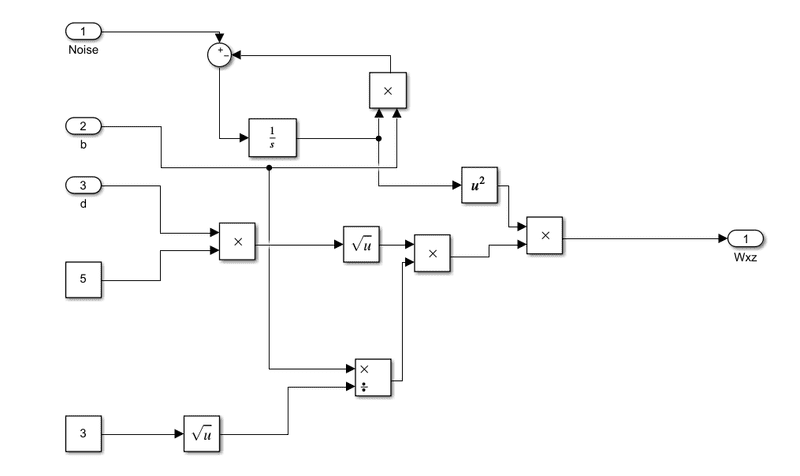
F1(s) = (((5d)^(1/2))*((b/sqrt(3))+s)) / (b+s)^2;

The implementations for the two filters in simulink are as follow:

For the first filter:

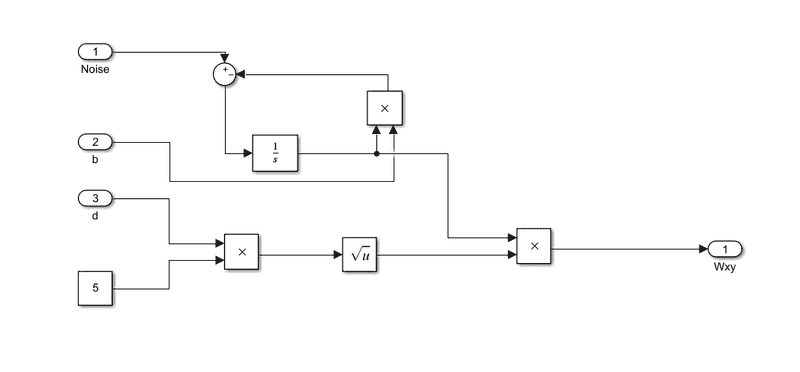
For the second one:

The obtained results have values of 10^-12, while the expected results should be between 10^-3 - 10.
Since it's the first time when I try t implement a tf with variable coefficients I am not sure the implementations are correct.

I don't understand how the block scheme should be made such that I would obtain sqrt(5d)/b+s.

 

[FactChecker]

I have worked with Tustin transformations whose parameters changed. I had to make my own blocks that had inputs for a reset flag, a flag to initialize with steady-state values, and the parameters (and of course, the input signal). The reset flag would recalculate the Tustin coefficients, the initialization flag would be set if the Tustin should be initialized in a steady state, and the parameters could be changed according to schedules. If the initialization flag is set, the behavior of the transformation is momentarily just a pass-through of the input signal. If the initialization flag is not set, the output would simply be calculated as though the transformation was active, regardless of whether the parameters had changed or not.

 

[MoonDiver]

I have worked with Tustin transformations whose parameters changed. I had to make my own blocks that had inputs for a reset flag, a flag to initialize with steady-state values, and the parameters (and of course, the input signal). The reset flag would recalculate the Tustin coefficients, the initialization flag would be set if the Tustin should be initialized in a steady state, and the parameters could be changed according to schedules. If the initialization flag is set, the behavior of the transformation is momentarily just a pass-through of the input signal. If the initialization flag is not set, the output would simply be calculated as though the transformation was active, regardless of whether the parameters had changed or not.

Thank you for the response!

What I don't understand is how should the block scheme look like in order to achieve the b + s part of the function.

F(s) = 5d^(1/2)/(b + s)