How to Implement Control for an Inverted Pendulum System?

[thegreengineer]

Good afternoon people. I wanted to implement a physical system using control just to put into practice what I have learned in school. To be more specific: I would like to implement an inverted pendulum like the one on the photo

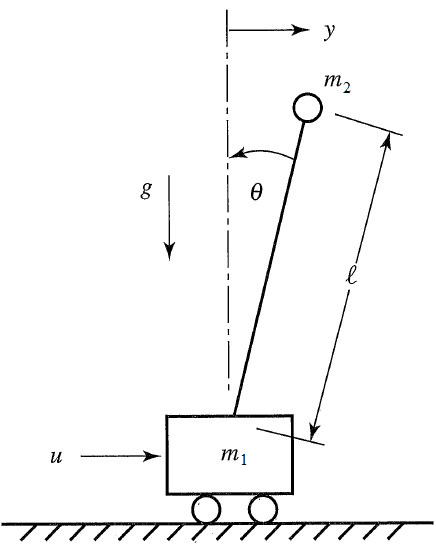
In this system a control input (a force u) drives the cart (mass m1) which moves the massless rod (with l) with a mass m2 attached at the end. The goal is to keep the mass m2 vertical by making the control output (an angle θ) zero.
The control paradigm I would like to use is modern control, which means I would require first to derive the differential equations of the system; then identify control input, control output, and state variables, in order to find the state and output equations we all know:
\mathbf{\dot{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}u
\mathbf{y}=\mathbf{C}\mathbf{x}+\mathbf{D}u
The next series of steps would be determining controllability, observability. After that then building the gain matrix K and (if necessary) build the observer. The result would be a block diagram like this:

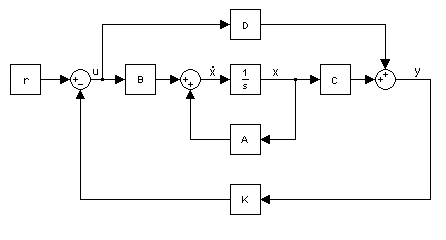
My main questions would be: where do other elements like sensors and actuators (like a rotary encoder and a motor) be in the block diagram? Would they be part of the plant (the inverted pendulum) block that includes the A, B, C and D matrices? or would they be treated outside the plant?
Also how would the controller be implemented? Is it an electrical network made of opamps? Is it a mechanical system? What is it? The same would be for how an observer would be implemented on a real system.

This is the main disadvantage I see about using modern control instead of classic control, since classic control deals with transfer functions and I could easily see where the sensor, the actuator, the plant and other signal conditioning blocks would fit:

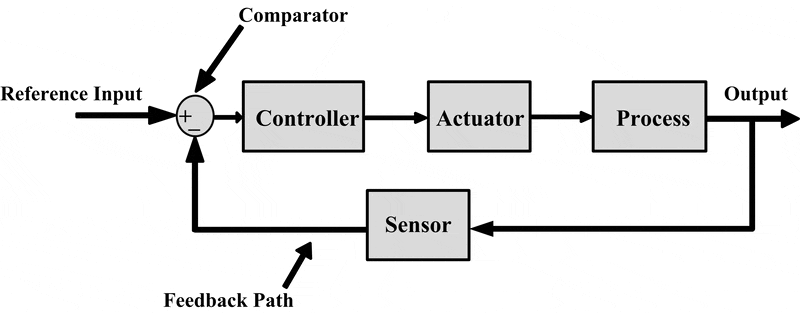
Easily the input could be a voltage (corresponding to the angle), the controller could be a PID controller made with op-amps, the actuator could be a motor, the process is the inverted pendulum, the sensor could be a rotary encoder or a potentiometer, and the output could be the output angle. Other elements like amplifiers, filters, and so on could be put between the controller and the actuator. Also the comparator could be an electronic op-amp since the input and feedback path signals are electrical in nature.

I would appreciate your answers to this problem.

 

[anorlunda]

The inverted pendulum is notoriously difficult because it is unstable. The most successful control approach with inverted pendulums is not classical, nor modern, it is fuzzy logic. Are you familiar with that?

Search "fuzzy logic" "inverted pendulum" and you'll find lots of hits.

 

[thegreengineer]

The inverted pendulum is notoriously difficult because it is unstable. The most successful control approach with inverted pendulums is not classical, nor modern, it is fuzzy logic. Are you familiar with that?

Search "fuzzy logic" "inverted pendulum" and you'll find lots of hits.

Ok, but that doesn't answer my questions. Let's imagine the plant could have been other dynamic system like a robotic arm, a liquid level system, a system in general. The questions were:
Where do other elements like sensors and actuators be in the block diagram? Would they be part of the plant block that includes the A, B, C and D matrices? or would they be treated outside the plant?
Also how would the controller be implemented? Is it an electrical network made of opamps? Is it a mechanical system? What is it? The same would be for how an observer would be implemented on a real system.

 

[Asymptotic]

Also how would the controller be implemented? Is it an electrical network made of opamps? Is it a mechanical system? What is it?

What do you want it to be?

You may consider doing a search on "inverted pendulum control project", and see how others have approached the problem.

 

[anorlunda]

Where do other elements like sensors and actuators be in the block diagram?

Sensors and actuators convert one kind of signal to another. Perhaps electrical to/from mechanical. Most often, we depict them in the block diagrams as a transfer function of 1, so they don't need to appear at all. But if they have a transfer function other than one, they need to be included as in the block diagram you posted.

The controller can be anything, electrical, mechanical, pneumatic, or digital. In the modern world, digital controllers (meaning computers) are frequently used. It is up to the engineer designing the system to choose what type of controller to use based on its total advantages.