How to prove that electric field propagates like a wave?
- Thread starter Adesh
- Start date
Click For Summary
SUMMARY
The discussion centers on the propagation of electric fields as waves, referencing Feynman Lectures on Physics Volume 1, specifically chapter 29. It establishes that static electric fields, such as those from a charge Q, do not propagate like waves, while changing electric and magnetic fields can create self-sustaining electromagnetic waves. The wave equations for electric and magnetic fields in vacuum are given as ∂²E/∂t² - c²∇²E = 0 and ∂²B/∂t² - c²∇²B = 0, highlighting the significance of the second time derivative in defining wave behavior.
PREREQUISITES- Understanding of electromagnetic fields, including static and propagating types.
- Familiarity with wave equations in physics.
- Knowledge of Feynman Lectures on Physics, particularly chapter 29.
- Basic calculus, specifically partial derivatives.
- Study the derivation of wave equations for electromagnetic fields in vacuum.
- Explore the implications of the second time derivative in wave mechanics.
- Investigate the relationship between electric and magnetic fields in changing conditions.
- Review Coulomb's law and its limitations in describing dynamic electromagnetic phenomena.
Physics students, educators, and professionals interested in electromagnetic theory and wave propagation, particularly those studying or teaching advanced concepts in electromagnetism.
Similar threads
- · Replies 2 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 4 ·
- · Replies 3 ·
- · Replies 1 ·
High School
Interpreting light as Maxwell's EM wave
- · Replies 65 ·
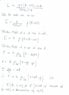

 ,
,