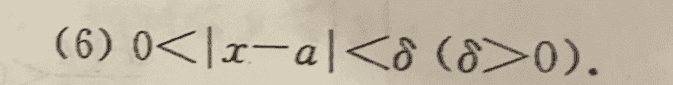SUMMARY
The discussion focuses on representing the absolute value inequality \(0 < |x - a| < \delta\) graphically on the x-axis. Participants clarify that the constant "a" does not require separation into different cases, as it is not conditioned. Instead, a single interval representation, \( (a - \delta, a + \delta) \), suffices to illustrate the concept. Additionally, the correct notation for excluding points, such as \(x = a\), involves using round brackets in the interval notation.
PREREQUISITES
- Understanding of absolute value inequalities
- Familiarity with interval notation
- Basic graphing skills on the x-axis
- Knowledge of epsilon-delta definitions in calculus
NEXT STEPS
- Study the epsilon-delta definition of limits in calculus
- Learn about interval notation and its graphical representation
- Explore how to graph inequalities on the x-axis
- Investigate the implications of excluding points in interval notation
USEFUL FOR
Students learning calculus, mathematics educators, and anyone interested in understanding graphical representations of inequalities.