How to 'shift' Fourier series to match the initial condition of this PDE?

[Master1022]

Homework Statement

How can I match the following Fourier series to match the initial condition for a PDE?

Relevant Equations

Fourier Series

Hi,

Question: If we have an initial condition, valid for $-L \leq x \leq L$:
$$f(x) = \frac{40x}{L}$$ how can I utilise a know Fourier series to get to the solution without doing the integration (I know the integral isn't tricky, but still this method might help out in other situations)?

We are given the following Fourier series:
$$\frac{2A}{\pi} \left( sin(\phi) + \frac{1}{2} sin(2 \phi) + \frac{1}{3} sin(3\phi) + ... \right)$$ where $\phi = \frac{2 \pi x}{T}$ and $A$ is the amplitude. This represents a function that looks like this (this would be sharper with more terms, but I just put a few into Desmos):

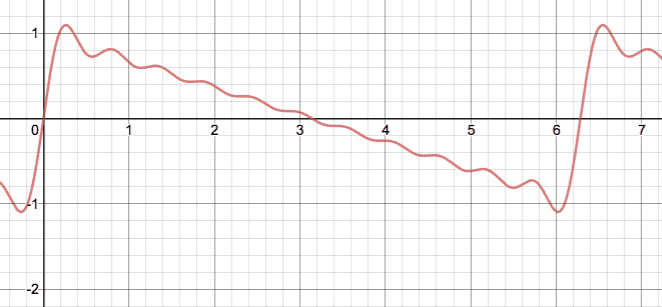
My attempt:
I think we want to do the following steps:
1. Reflect the series about the x-axis (multiply by -1)
2. Shift/scale the series have a zero at the origin and have a full period range from $-L$ to $L$

It is the second step that confuses me and I am not completely sure how to do it, but this is how I approached it:
- we want the point where $\pi$ is to shift to the origin (so $\phi + \pi$)
then we get that $sin(\phi + \pi) = -sin(\phi)$.
- then we let T = 2L to get and A = 40 to get:
$$\frac{-2\times 40}{\pi} \left(-sin(\frac{\pi x}{L}) + \frac{1}{2} sin(\frac{2 \pi x}{L}) - \frac{1}{3} sin(\frac{3 \pi x}{L}) + ... +\frac{(-1)^n}{n}sin(\frac{n \pi x}{L}) \right)$$

Does this method seem correct?

However, what if there is a shift and scale required? How does that change the order of the transformation? Should we always do the shift first, for out the trig double angle simplification, and then do the scaling in the x-direction?

Any help is greatly appreciated.

 

[pasmith]

If you need an affine transformation, then you should do that in a single step: $$[a,b] \to [0, 2\pi]: x \mapsto \frac{2\pi}{b - a}(x - a).$$ Thus here $$\phi = \frac{\pi}L (x + L), \qquad x = -L + \frac{L}{\pi} \phi$$ and $$\frac{40x}{L} = -40 + \frac{40}{\pi} \phi.$$

 

[Master1022]

If you need an affine transformation, then you should do that in a single step: $$[a,b] \to [0, 2\pi]: x \mapsto \frac{2\pi}{b - a}(x - a).$$ Thus here $$\phi = \frac{\pi}L (x + L), \qquad x = -L + \frac{L}{\pi} \phi$$ and $$\frac{40x}{L} = -40 + \frac{40}{\pi} \phi.$$

Thank you for your reply! Okay, this method makes sense. However, why did you substitute in the expression for $x$ into the initial condition? I suppose that might be feasible if the $\phi$ was defined within the problem?

I think for this case, I would just use the expression $\phi = \frac{\pi}L (x + L)$ and substitute into the Fourier series to have a match to my initial condition? I think you know that though, I just wanted to confirm. By substituting in your expression for $\phi$ to the Fourier series, it yields the same trig identity so that is very re-assuring.

Thanks

 

[Master1022]

If you need an affine transformation, then you should do that in a single step: $$[a,b] \to [0, 2\pi]: x \mapsto \frac{2\pi}{b - a}(x - a).$$ Thus here $$\phi = \frac{\pi}L (x + L), \qquad x = -L + \frac{L}{\pi} \phi$$ and $$\frac{40x}{L} = -40 + \frac{40}{\pi} \phi.$$

Sorry to bring this back up, but what if the original wave described by the Fourier series was shifted by $\pi$ (or any other phase)? Would I then:
1) use a phase shift $\phi = \phi + \pi$ to shift the Fourier series wave to where I want
2) expand with double angle formula and simplify
3) use the affine transformation to map from $\phi$ to $x$

Would that process be correct?

Thank you

 

[pasmith]

Thank you for your reply! Okay, this method makes sense. However, why did you substitute in the expression for $x$ into the initial condition? I suppose that might be feasible if the $\phi$ was defined within the problem?

It's the natural thing to do: To evaluate $$\int_a^b f(x) \sin\left(\frac{2n\pi(x - a)}{b - a}\right)\,dx = \frac{b - a}{2\pi}\int_0^{2\pi} f\left(a + \frac{(b-a)}{2\pi}\phi\right) \sin(n\phi)\,d\phi$$ one has to. Also, in this special case of a linear boundary condition, it is obvious from $$\frac{40x}{L} = -40 + \frac{40}{\pi}\phi$$ that the initial condition is -40 plus $(40/\pi)$ times the unshifted series for $\phi$. This is easier to calculate than the shifted series.