evol_w10lv
- 70
- 0
Homework Statement
I have got double contour integral:
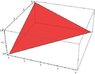
And here is picture:
I know every line equation as well.
The task is to calculate this integral as:
1. surface integral of outside of the area (in the picture)
2. using Ostrogradsky formula
Homework Equations
Equation of plane: 4x+3y+12z-12=0
It means that x=3-0.75y-3z and z=1-0.25y-(1/3)x
The Attempt at a Solution
I guess, this can be integral for task 1, when we use surface integral:
Can someone chek, if it's correct? And how to start task 2, when I have to use Ostrogradsky formula?