DLeuPel
- 56
- 2
I’m trying to figure out how logarithms we’re invented. In addition, what does the calculator do when I want to solve a logarithm. After researching I found out that you could compare an arithmetic progression with a geometrical one, obtaining the principal properties of exponent calculation. Later, I found that Napier imagined a segment AB, where there was a point Q traveling along the segment but it’s velocity decreased proportionally in relation to the distance left to reach B. This would be a geometric progression. Then, you would divide the segment for each second that passed. After that, you would stretch the divided parts so they are equal. So due to the fact that the velocity decreases in relation to the distance left to B, it never reaches B. Therefore, the distance to B is infinite since for each second, the point travels the same distance. This would be an arithmetical progression.
Until there I can sort of understand it, but the difficult part for me comes here:
—————- The point
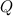 moves at a constant speed of 107, so we have
moves at a constant speed of 107, so we have
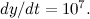 Since P moves at a speed that is proportional to the distance
Since P moves at a speed that is proportional to the distance
 left to travel we have
left to travel we have
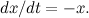 From this we see that
From this we see that
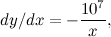
which gives
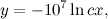
for some constant
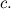
We can work out the value of c using our initial conditions. At the start, the point P still needs to travel the whole length of the line segment AB, which is 107. Therefore
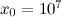 . The point Q hasn’t gone anywhere yet, so
. The point Q hasn’t gone anywhere yet, so
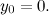
Plugging this into the expression above gives
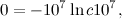
so
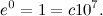
Therefore,
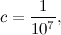
so
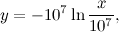
and
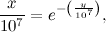 ————-
————-
All of the calculations on the top are copied from https://plus.maths.org/content/calculating-napiers-logarithm
Now, if we are trying to solve or to figure out how were logarithms invented and imagined, how does the ln appear if that itself is a logarithm. Also, could someone complete the explication of the foundation of logarithms ?
Until there I can sort of understand it, but the difficult part for me comes here:
—————- The point
which gives
for some constant
We can work out the value of c using our initial conditions. At the start, the point P still needs to travel the whole length of the line segment AB, which is 107. Therefore
Plugging this into the expression above gives
so
Therefore,
so
and
All of the calculations on the top are copied from https://plus.maths.org/content/calculating-napiers-logarithm
Now, if we are trying to solve or to figure out how were logarithms invented and imagined, how does the ln appear if that itself is a logarithm. Also, could someone complete the explication of the foundation of logarithms ?
Attachments
-
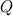 img-0002.png227 bytes · Views: 509
img-0002.png227 bytes · Views: 509 -
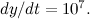 img-0004.png477 bytes · Views: 569
img-0004.png477 bytes · Views: 569 -
 img-0006.png162 bytes · Views: 544
img-0006.png162 bytes · Views: 544 -
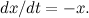 img-0007.png404 bytes · Views: 512
img-0007.png404 bytes · Views: 512 -
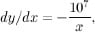 img-0008.png544 bytes · Views: 561
img-0008.png544 bytes · Views: 561 -
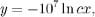 img-0009.png439 bytes · Views: 554
img-0009.png439 bytes · Views: 554 -
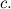 img-0010.png164 bytes · Views: 484
img-0010.png164 bytes · Views: 484 -
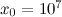 img-0013.png318 bytes · Views: 561
img-0013.png318 bytes · Views: 561 -
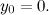 img-0014.png280 bytes · Views: 590
img-0014.png280 bytes · Views: 590 -
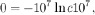 img-0015.png406 bytes · Views: 522
img-0015.png406 bytes · Views: 522 -
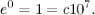 img-0016.png379 bytes · Views: 521
img-0016.png379 bytes · Views: 521 -
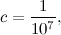 img-0017.png299 bytes · Views: 531
img-0017.png299 bytes · Views: 531 -
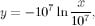 img-0018.png515 bytes · Views: 527
img-0018.png515 bytes · Views: 527 -
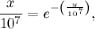 img-0001.png539 bytes · Views: 553
img-0001.png539 bytes · Views: 553