- #1
Rectifier
Gold Member
- 313
- 4
The problem
I am trying to calculate the integral $$ \int_{\gamma} \frac{z}{z^2+4} \ dz $$
Where ## \gamma ## is the line segment from ## z=2+2i ## to ## z=-2-2i ##.
The attempt
I would like to solve this problem using substitution and a primitive function to ## \frac{1}{u} ##. I am not interested in alternative ways of solving this problem right now, thank you for your understanding.
## \int_{\gamma} \frac{z}{z^2+4} \ dz = [u=z^2+4 \, \ \ du = 2z dz] = \\
= \frac{1}{2} \int_{\gamma} \frac{1}{u} \ du = \frac{1}{2} \left[ log(u) \right]_{\gamma} ##
## log(u) = ln|u| + iarg(u) ##
The trouble is: I am not used to line segments that pass through the origin. I don't now which branch to choose for the argument of the complex logarithm since I was thought that when you make the cuts for the branches you cut out 0 and go to infinity on one of the axes. (Is that perhaps wrong?)
Example:
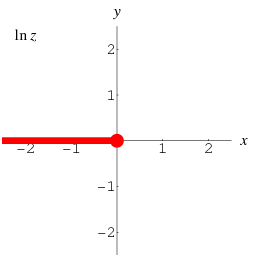
Principal branch for angles ##-\pi<Arg<\pi##
How do I proceed?
I am trying to calculate the integral $$ \int_{\gamma} \frac{z}{z^2+4} \ dz $$
Where ## \gamma ## is the line segment from ## z=2+2i ## to ## z=-2-2i ##.
The attempt
I would like to solve this problem using substitution and a primitive function to ## \frac{1}{u} ##. I am not interested in alternative ways of solving this problem right now, thank you for your understanding.
## \int_{\gamma} \frac{z}{z^2+4} \ dz = [u=z^2+4 \, \ \ du = 2z dz] = \\
= \frac{1}{2} \int_{\gamma} \frac{1}{u} \ du = \frac{1}{2} \left[ log(u) \right]_{\gamma} ##
## log(u) = ln|u| + iarg(u) ##
The trouble is: I am not used to line segments that pass through the origin. I don't now which branch to choose for the argument of the complex logarithm since I was thought that when you make the cuts for the branches you cut out 0 and go to infinity on one of the axes. (Is that perhaps wrong?)
Example:
Principal branch for angles ##-\pi<Arg<\pi##
How do I proceed?