Hauzen
- 13
- 4
Hi!
I have a loss head question.
There is a difficulty in understanding the hydrodynamic loss head concept.
Assuming that there is a one-sided tube with incompressibility, visibility, tube friction coefficient and cross-sectional area A..
There is friction in the loss head formula, but is the flow rate and flow rate of the Inlet and Oulets the same?
I know that continuous equations are useful when there is no friction.
I don't understand that there is friction, but the flow rate of the Oulet does not decrease. And in the loss head, it is stated that v is the average velocity, but is it the v of the inlet? Is it the v of the outlet?
I don't understand the concept exactly.
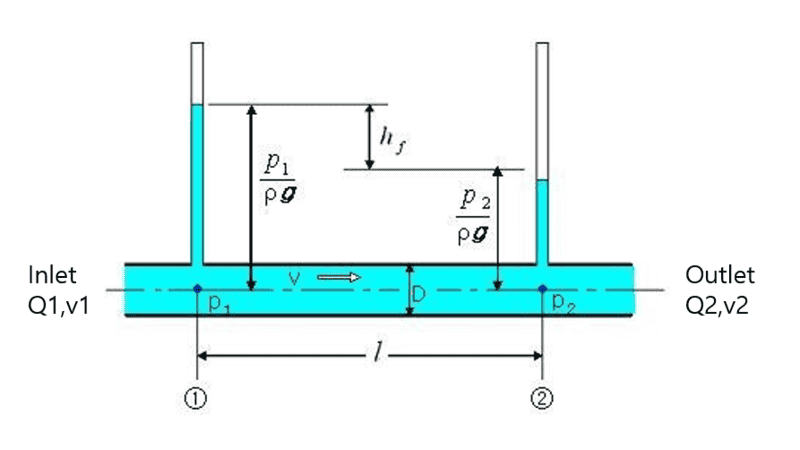
I have a loss head question.
There is a difficulty in understanding the hydrodynamic loss head concept.
Assuming that there is a one-sided tube with incompressibility, visibility, tube friction coefficient and cross-sectional area A..
There is friction in the loss head formula, but is the flow rate and flow rate of the Inlet and Oulets the same?
I know that continuous equations are useful when there is no friction.
I don't understand that there is friction, but the flow rate of the Oulet does not decrease. And in the loss head, it is stated that v is the average velocity, but is it the v of the inlet? Is it the v of the outlet?
I don't understand the concept exactly.
Last edited by a moderator: