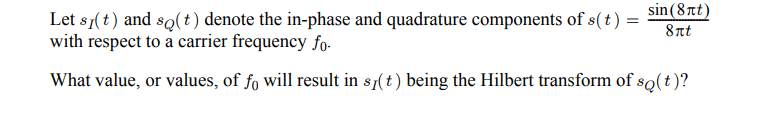Hi, just thought I would give this a go because it is unanswered.
ashah99 said:
I can find the Fourier Transform of the complex envelope of s(t) and the I/Q can be found by taking the Real and imaginary parts of that complex envelope, but how can I approach the actual question of finding the carrier f0?
Apologies, would you mind explaining how you find the in-phase and quadrature-phase components of the signal. If I had to make an educated guess (let me know if I am wrong), I thought we would try to resolve onto the in-phase and quadrature signals. That is, if we defined cos as in-phase and sin as quadrature-phase something along the lines of:
\text{In-phase component } s_{I}(t) = \int s(t) cos(2\pi f_0 t) dt
and
\text{Quadrature-phase component } s_{Q}(t) = \int s(t) sin(2\pi f_0 t) dt
(or we could define them the other way around)
Before I type out the rest of the what I did does that seem reasonable (otherwise, I don't want to lead you astray)?
IF that seems fair, then those integrals look like Fourier transform integrals evaluated at ## f = 0 ##... and we know that the
Fourier transform of a product in the time domain is the product of the Fourier transforms in the frequency domain...
- By duality we can find Fourier transform of s(t)
- We know the Fourier transforms of the ##sin(2 \pi f_0 t)## and ##cos(2\pi f_0 t)## for a general ## f_0 ##
- We could calculate the convolution for both in-phase and quadrature-components
If you agree with the above (feel free to correct and/or disagree with me), then we can apply the Hilbert transform visually to look where the two