Ideal Gas Question in Thermodynamics

[jrklx250s]

Homework Statement

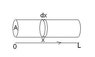
Given the temperature of an ideal gas in a tub where it varies linearly from (x=0) to (x=L)

T = To + [(TL - To)/L]x

where To is temperature at 0 length and TL is the temperature at the end of the tube

We are suppose to show that the equation of state for this ideal gas is

PV=nR[(TL-To)/ln(TL/To)]

As well as if then To = TL = T show that the equation of state reduces to the obvious one...PV=nRT

The Attempt at a Solution

So first off I wasnt sure of where to start because I know the only changing variable in this question is temperature so I know we are suppose to rearrange this equation
T = To + [(TL - To)/L]x

However I'm not sure on how to derive this equation.
Mostly this is alegbra/dervatives/integration problem.
And I'm honestly stuck as to where to go from the temperature equation
Any suggestions on where to begin would be greatly appreciative.

 

[ehild]

The gas is in rest so the pressure has to be constant in the whole volume, but the density of the gas changes according to the ideal gas law.
Write out the density as function of x and the constant pressure P and integral for the whole volume to get the amount of gas. ehild

 

[jrklx250s]

Thanks for your reply, so I'm a little confused, the density is changing therefore we can write

σ(x) = Pdx
∫σ(x) = P∫dx
∫σ(x) = P(xL-x0)

But how does this help with the temperature equation?

 

[ehild]

Thanks for your reply, so I'm a little confused, the density is changing therefore we can write

σ(x) = Pdx
∫σ(x) = P∫dx
∫σ(x) = P(xL-x0)

But how does this help with the temperature equation?

I do not know what your equation means, I thought of the ideal gas law, I guess you know what it is? And density as mass/volume.

ehild

 

[jrklx250s]

Indeed,

PV=nRT

But my main question is how to derive T = To + [(TL - To)/L]x
To eventually make it into T = [(TL-To)/ln(TL/To)]

I'm lost as to where to even start in this derivation

 

[ehild]

Indeed,

PV=nRT

But my main question is how to derive T = To + [(TL - To)/L]x
To eventually make it into T = [(TL-To)/ln(TL/To)]

I'm lost as to where to even start in this derivation

T = To + [(TL - To)/L]x is given, you can not derive it.

The problem is to find the equation of state of the ideal gas in that tube. That means the relation between P, V, he number of moles, and a quantity, you can call an effective temperature. The method is that you consider the tube as a couple of cells, each at the same pressure, and temperature as given at the position of the cell. You need to find the number of moles in each cell. For that, apply the ideal gas law PV=nRT for the cells. The number of moles in a volume element dV is equal to the density of moles multiplied by dV.
The density σ changes with temperature along the length of the tube, so you need a relation between temperature and density. σ=n/V. How is σ related to P and T?

ehild

 

[jrklx250s]

Well since density is number of moles over volume
σ = n/v

and V = nRT/P

σ= P/RT

but I am unsure how this helps me because now I have the density at x=0 which is P/RTo and the density at x=L which is P/RTL

 

[ehild]

Well since density is number of moles over volume
σ = n/v

and V = nRT/P

σ= P/RT

but I am unsure how this helps me because now I have the density at x=0 which is P/RTo and the density at x=L which is P/RTL

You have the density at every x if you substitute T = To + [(TL - To)/L]x into σ= P/RT. From the density at x, you can calculate the number of moles in a small slice of the tube of volume dV=Adx: it is dn=σdV. If you integrate dn with respect to x from x=0 to x=L, you get the number of moles in the tube, which has the volume V=AL.


ehild

 

[ehild]

I do not like when an interesting thread is interrupted without any feedback, so I do a few steps steps forward; hopefully, I will be more clear now.

The molar density of gas at x is n/V=σ=P/(RT)

The temperature was given as T(x) = To + [(TL - To)/L]x. Introducing the notation

b=(TL/To - 1)/L,

T(x)=To(1+bx).

Substituting for T(x) in the expression for the density:

σ=\frac{P}{RTo}\frac{1}{1+bx}

Taking a volume element as a slice of the tube with cross-section A and thickness dx, the number of moles in that volume is dn=σAdx. To get the number of moles in the tube, integrate dn with respect to x from 0 to L.

n=\frac{PA}{RTo} \int_0^L{\frac{1}{1+bx}dx}=\frac{PA}{bRTo} ln(1+bL)

Replacing back b=(TL-To)/(ToL), and using that AL=V, the volume of the gas,

n=\frac{PALTo}{(TL-TO)RTo} ln(1+(TL-To)/To)=\frac{PV}{R}\frac{ln(TL/To)}{TL-To}.

From here, the equation of state is obtained in the form PV=nRT_eff, where T_eff is some effective temperature, characterising the gas in the tube.

ehild