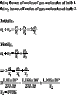fluppocinonys
- 19
- 1
Two glass bulbs of equal volume are joined by a narrow tube and are filled with gas at s.t.p. (standard temperature and pressure where \theta = {0^ \circ }{\rm{C}} and p = 1.01 \times {10^5} Pa). When one bulb is kept in melting ice and the other is placed in hot bath, the new pressure is 1.166 x 105 Pa. Calculate the temperature of the bath.
I tried to use
\begin{array}{l}<br /> \frac{{{p_1}{v_1}}}{{{T_1}}} = \frac{{{p_2}{v_2}}}{{{T_2}}} \\ <br /> {v_1} = {v_2} \\ <br /> \frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \\ <br /> \end{array}
but failed to arrive at the answer. The answer is 370K
Can anyone guide me? Thanks.
I tried to use
\begin{array}{l}<br /> \frac{{{p_1}{v_1}}}{{{T_1}}} = \frac{{{p_2}{v_2}}}{{{T_2}}} \\ <br /> {v_1} = {v_2} \\ <br /> \frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \\ <br /> \end{array}
but failed to arrive at the answer. The answer is 370K
Can anyone guide me? Thanks.