eddywalrus
- 25
- 0
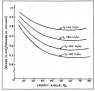
I recently read that the impact of air resistance on the horizontal range increases as the launch angle increases (http://moodle.davidson.edu/moodle2/pluginfile.php/121168/mod_resource/content/2/Brancozio%20fly-ball%20paper.pdf). A graph depicting this is attached. Is there a reason for why this is? I'm not a very good mathematician so it would be great if the explanations didn't involve too much calculus / are mainly qualitatitive (although I do understand a bit of differentiation and integration)
Attachments
Last edited: