The Tortoise-Man
- 95
- 5
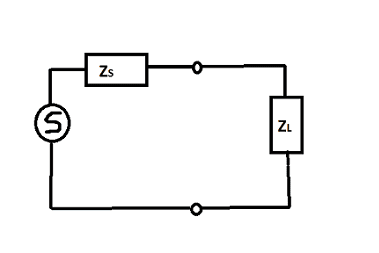
Assume we have a network consisting of a source with impedance ##Z_S## and load with impedance ##Z_L## and
we want to perform impedance matching on them in order to obtain the maximum power transfer:
Note that in practice there may occur sitations where causes more harm than profit (see eg Baluncore's example here: https://www.physicsforums.com/threa...g-when-the-transmitter-line-and-load.1009889/ ; see post #2)But the motivation of this question has pure conceptional nature; ie I'm not asking here IF it should be done but HOW it should be correctly done, if one has to do it.
In general, ##Z_S \neq Z_L^*##. So principally, what one do in order to match impedances, one places a matching network between source and load (the components which the matching network contains depend on concrete problem):
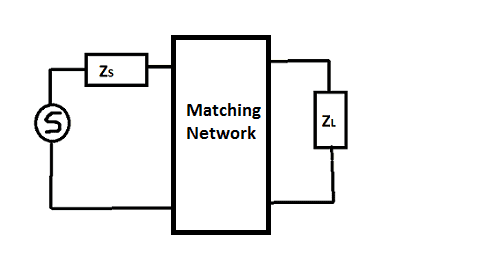
Indeed, the matching network can consist of resistive components, it might be a L- or T-network and and and... ) and one tries to adjust the parameters of the components of the matching network to satisfy certain matching conditions; see below.
Now having implemented the matching network in our circuit in order to impose the right mathematical conditions we introduce following two auxilary impedances: the input impedance ##Z_{in}## and output impedance ##Z_{out}## defined as follows:
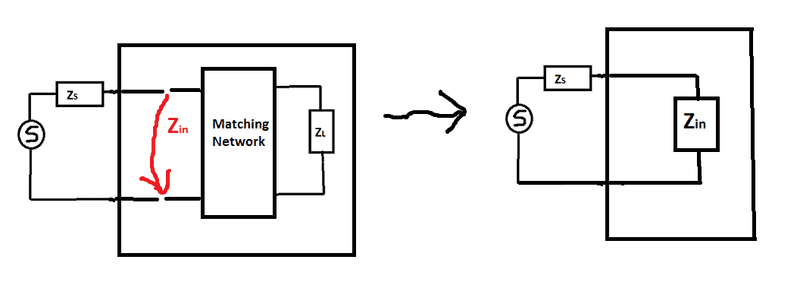
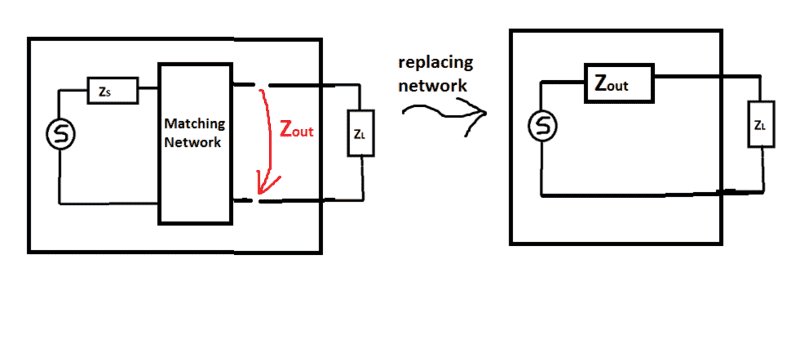My question is: In order to obtain the impedance matching
for maximal power transfer which conditions should be satisfied?
##Z^*_s= Z_{in}##, ##Z_{out}= Z^*_L## or both simultaneously?
Or even more interesting question is: Assume we succeed in adaping the components within the matching network such that ##Z^*_s= Z_{in}## holds. Is then ##Z_{out}= Z^*_L##
automatically satisfied?
So the question is basically about if it really neccassary to adapt the components within the matching network such that they should satisfy both conditions ##Z^*_s= Z_{in}## AND ##Z_{out}= Z^*_L##, or is one of these conditions really redundant in the sense that it suffice to adjust the matching box only to satisfy ONE of them and the second is the satisfied automatically?
we want to perform impedance matching on them in order to obtain the maximum power transfer:
Note that in practice there may occur sitations where causes more harm than profit (see eg Baluncore's example here: https://www.physicsforums.com/threa...g-when-the-transmitter-line-and-load.1009889/ ; see post #2)But the motivation of this question has pure conceptional nature; ie I'm not asking here IF it should be done but HOW it should be correctly done, if one has to do it.
In general, ##Z_S \neq Z_L^*##. So principally, what one do in order to match impedances, one places a matching network between source and load (the components which the matching network contains depend on concrete problem):
Indeed, the matching network can consist of resistive components, it might be a L- or T-network and and and... ) and one tries to adjust the parameters of the components of the matching network to satisfy certain matching conditions; see below.
Now having implemented the matching network in our circuit in order to impose the right mathematical conditions we introduce following two auxilary impedances: the input impedance ##Z_{in}## and output impedance ##Z_{out}## defined as follows:
for maximal power transfer which conditions should be satisfied?
##Z^*_s= Z_{in}##, ##Z_{out}= Z^*_L## or both simultaneously?
Or even more interesting question is: Assume we succeed in adaping the components within the matching network such that ##Z^*_s= Z_{in}## holds. Is then ##Z_{out}= Z^*_L##
automatically satisfied?
So the question is basically about if it really neccassary to adapt the components within the matching network such that they should satisfy both conditions ##Z^*_s= Z_{in}## AND ##Z_{out}= Z^*_L##, or is one of these conditions really redundant in the sense that it suffice to adjust the matching box only to satisfy ONE of them and the second is the satisfied automatically?