- #1
The Tortoise-Man
- 95
- 5
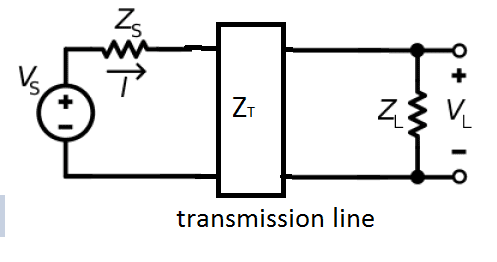
Assume we have a general rf system where source with impedance ##Z_S##
transfers a signal to a load with impedance ##Z_L## through a transmission
line with impedance ##Z_T##. We want to match this system
in order to maximize it's effiency:
In
https://en.wikipedia.org/wiki/Impedance_matching
there are two options how to do it if we deal with power transfer
from source to load through a transmission line:
There is one way to to maximize the power transfer; the
condition that should be fulfilled is ##Z_S = Z^*_L## and on the
other hand there is a way to minimize the reflexion of the signal waves.
To do this the relations between the source and transmission line
should satisfy ##Z_S=Z_T## and and between
load and transmission line ##Z_L=Z_T##.
Obviously, it is not possible (if the system contains reactant components)
to fulfill both conditions, ie to maximize the power transfer AND
to minimize the signal wave reflexion.
My question is what to do in such situation? How to decide what to do
here in order to run the system with best effiency? How to decide
what is more important: to maximize the power transfer or
to minimize the signal wave reflexion? Is there a kind of guide
how to decide in such or similar cases?
transfers a signal to a load with impedance ##Z_L## through a transmission
line with impedance ##Z_T##. We want to match this system
in order to maximize it's effiency:
In
https://en.wikipedia.org/wiki/Impedance_matching
there are two options how to do it if we deal with power transfer
from source to load through a transmission line:
There is one way to to maximize the power transfer; the
condition that should be fulfilled is ##Z_S = Z^*_L## and on the
other hand there is a way to minimize the reflexion of the signal waves.
To do this the relations between the source and transmission line
should satisfy ##Z_S=Z_T## and and between
load and transmission line ##Z_L=Z_T##.
Obviously, it is not possible (if the system contains reactant components)
to fulfill both conditions, ie to maximize the power transfer AND
to minimize the signal wave reflexion.
My question is what to do in such situation? How to decide what to do
here in order to run the system with best effiency? How to decide
what is more important: to maximize the power transfer or
to minimize the signal wave reflexion? Is there a kind of guide
how to decide in such or similar cases?
Last edited: