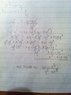- #1
JustinLiang
- 81
- 0
Homework Statement
Find y' in
e^(x/y)=x-y
2. The attempt at a solution
I tried to differentiate it by changing it so that there would be a natural log (as seen in my attachment). However the end result is not the same as the answer key.
How the answer key did it was they used the chain rule on e^(x/y). So...
e^(x/y)*(x/y)'=1-y'
And then they solve for y'.
Why can I not change the e^(x/y) to the logarithmic notation?
Attachments
Last edited: