Improving Electrical Supply System for Lower Fault MVA: Analysis and Solutions

[topcat123]

Homework Statement

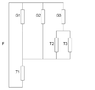
FIGURE 3 shows part of an electrical supply system.

Draw the impedance diagrams reducing to a single impedance.

Calculate the fault MVA levels in each unit for a fault on the left 3.3 kV bus with the bus section
switch B open and A closed. Use a base MVA of 10 and show
the fault MVA levels on a diagram.

Comment on the result and suggest a method of improving the system to limit the fault MVA through T1 to approximately 5 × FL current. (It is not necessary to recalculate.)

Homework Equations

The Attempt at a Solution

The fault MVA and pu impedances
$$G_1 and G_2\text{fault MVA} = \frac{16}{0.8}=20MVA$$
$$G_1 and G_2\text{ pu impedance} = \frac{10}{20}\frac{20}{100}=0.1pu$$
$$G_3\text{fault MVA} = \frac{1.6}{0.8}=2MVA$$
$$G_3\text{ pu impedance} = \frac{10}{2}\frac{20}{100}=1pu$$
$$T_1,T_2and T_3\text{ pu impedance} = \frac{10}{10}\frac{5}{100}=0.05pu$$
So we need to work out the total impedance and fault current.
$$T_2||T_3=0.025pu$$
$$G_3+T_2||T_3=1.025pu$$
$$(G_3+T_2||T_3)||G_1||G_2=0.0477pu$$
$$[(G_3+T_2||T_3)||G_1||G_2]+T_1=0.0977pu$$
So the fault MVA
$$\frac{10}{0.0977}=102.4MVA$$
So the fault MVA through T₁ is 102.4
and through the rest
$$\text{voltage MVA}(G_3+T_2||T_3)||G_1||G_2=102.4*0.0477=4.88MVA$$
Fault through G₁ and G₂
$$\frac{4.88}{0.1}=48.88MVA$$
Fault through G₃+T₂||T₃
$$\frac{4.88}{1.025}=4.76$$
$$\text{voltage MVA G₃}=4.76*1=4.76MVA$$
voltage MVA over T₂||T₃
$$=0.025*4.76=0.119MVA$$
Fault through T₂ and T₃
$$\frac{0.110}{0.05}=2.38MVA$$

I think this is correct.
The part I am struggling with is
"Comment on the result and suggest a method of improving the system to limit the fault MVA through T1 to approximately 5 × FL current. (It is not necessary to recalculate.)"

Any help would be appreciated.
Thanks

 

[MattSiemens]

Hi,
I have attempted the above question (before looking for help on here) and have the same answer as topcat123 for the first part, so assume I have calculated correctly.
I am to struggling on the second part of limiting the fault current through T1 to 5 x FL current.
I think I have found a way of doing this but this would be by changing the Voltage Impedance of T1 and also making use of a Reactor.
I am unsure if this is correct as changing the Voltage Impedance of T1 would effectively be changing the Transformer??
Any help would be appreciated.
Matt

 

[Babadag]

The calculation, it seems to me to be correct. However I did the calculation according to IEC 60909 also-using only reactances- and the difference is 2.5% less.
Since the system is isolated-that means no connection with the outside system ,even the generator voltages will be 11[3.3] kV the voltage on 11 kV bus decrease up to 5.365 kV[1.61 kV on 3.3 system] in the case of short-circuit when the short-circuit current will be Isc=102.4/sqrt(3)/3.3 =17.92 kA. and then the MVA on T1 will be sqrt(3)*17.92*1.69=52.424 MVA only.
So now the T1 load is 5.24 times the rated-at 17.92 kA.
If the transformer T1 impedance stays unchanged you have to reduce the current flowing through by 5/5.24[17.50 kA] by inserting a reactor in the T1 circuit [my opinion a series reactor of 0.00252 ohm/17.5 kA/3.3 kV ]