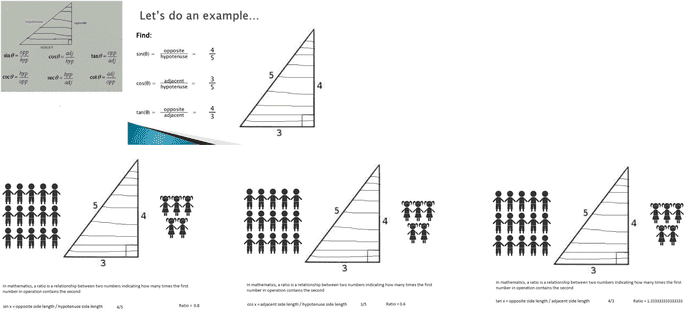
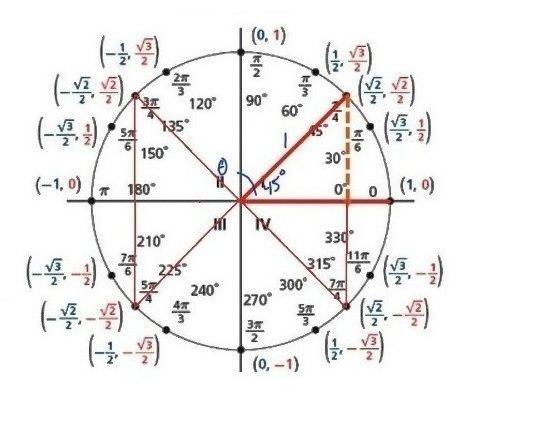
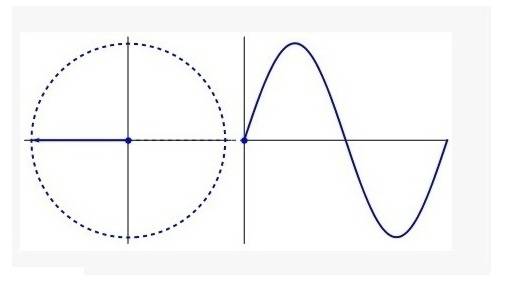
Are you ultimately trying to figure out how the right triangle relates to the unit circle and sine/cosine graphs? Is that it? Like on the images you posted above, you can see how right triangles can be found in a unit circle. You know how when you graph something each point is represented as ##(x,y)##? On a unit circle, we can see those same points as ##(\cos{t},\sin{t})##. To derive, say, a sine graph, we can take a Cartesian plane (a basic graphing plane) and replace the y-axis with ##\sin{\theta}## and the x-axis with ##\theta##. Now all we have to do is plot the points.
So, sticking to our sine graph (but cosine graphs are done the same way), when ##\theta=0^\circ## or radians, what is the value of sine? Remember how on a unit circle ##(x,y)## is the same as ##(\cos{t},\sin{t})##? So when ##\theta=0^\circ## on a unit circle, the coordinates are ##(1,0)## implying that ##\sin{0}## is 0, also. Thus, we have the first coordinate of out sine wave to be ##(0,0)##. Congratulations! We can continue to do this...when ##\theta=30^\circ##, or ##\frac{\pi}{6}## in radians, the point on the unit circle is ##(\frac{\sqrt{3}}{2},\frac{1}{2})##, telling us that ##\sin{30^\circ}=\frac{1}{2}##. Now we've got our second point for our sine graph: ##(30,0.5)##. If we keep doing this for the entire circle, we will eventually get one period of the sine wave. Hopefully this guy can illustrate it a bit more: