Incidences of refraction

[premed_love]

Homework Statement

I am preparing for a test. I really need help with this is problem. I uploaded a picture for the figure.
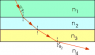
The figure below shows the path of a beam of light through several layers (n1 = 1.58, n2 = 1.39, n3 = 1.21 and n4 = 1.00) of different indices of refraction.

PART1 ASKS:
If

= 29.1o, what is the angle,

, of the emerging beam?

PART 2:
What must the incident angle,

, be in order to have total internal reflection at the surface between the n3 = 1.21 medium and the n4 = 1.00 medium?

Homework Equations

We have to use Snell's Law: which is n1sin=n2sin

The Attempt at a Solution

FOR PART 1: This is what I did:
I know N for 1 and 2. The angle is 29.1 as given. So...
[/B]

sin^-1=(n1/n2*sin) sin^-1=(1.58/1.39*sin29.1). I get .662 which is off.

For Part 2: I am clueless.

Please guide me.

 

[rude man]

sin^-1=(n1/n2*sin) sin^-1=(1.58/1.39*sin29.1). I get .662 which is off.

Your equation makes no sense to me. Try again? Start with Snell's law again, carefully.