Inclined plane with pulley and spring

[lorenz0]

Homework Statement

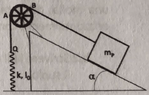
Consider a pulley which is a ring of radius $r$.
1) Find the moment of inertia of the pulley with respect to an axis through its center and perpendicular to its plane, knowing that the work needed to make the pulley rotate with angular momentum $L$ around this axis is $W$.
Now this pulley is placed on a frictionless inclined plane of angle $\alpha$, and an ideal rope connects a mass $m_p$ to a spring placed vertically to the left of the inclined plane, and with one end attached to the ground.
2) Find the length of the spring at equilibrium.
Starting from the equilibrium position we give to mass $m_p$ a speed $v_i$ parallel to the inclined plane and downwards.
If the rope doesn't slide on the pulley and always remains taut, find:
3) Period of the oscillation of the system.
4) The maximum and minimum value of the tension applied to the spring and to mass $m_p$.
5) The maximum value of the kinetic energy of the system.

Relevant Equations

$\sum_{i}\vec{F}_i=m\vec{a},\ W=\Delta K=K_f-K_i,\ F_{spring}=-ks,\ T=\frac{2\pi}{\omega}.$

1) By the Work-Energy Theorem, $W=K_f-K_i=\frac{1}{2}I_{0}\omega^2=\frac{L^2}{2I_0}.$
2) By assuming that the initial length of the spring is $0$, calling its final length $S$ and $T$ the tension in the rope connecting the pulley and mass $m_p$ I have: $\begin{cases}(kS-T)r=0\\ m_p g\sin(\alpha)-T=0 \end{cases}$ which gives $S=\frac{m_pg\sin (\alpha)}{k}.$
3) mass $m_p$ oscillates around the equilibrium position, so by denoting $s$ the displacement of $m_p$ from the equilibrium position I get $-ks=m_p s''\Rightarrow s''=-\frac{k}{m_p}s\Rightarrow \omega=\sqrt{\frac{k}{m_p}}\Rightarrow T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m_p}{k}}.$

Is it justifiable to ignore $T$ and $-ks$ since they "cancel out" each other because of the motion starting from the equilibrium position found before?

Thanks.

 

[Charles Link]

What about the pulley and its effect on the frequency? They should have given you a value for the mass of the pulley=call it $m_o$.

In addition, for part (3), I think the forces on $m_p$ are more complex than what you have. On $m_p$ you have the tension from the rope, and the force of gravity, i.e. the component along the incline. You then have the tension in the rope, (that is not the same everywhere), affected by how much the spring is stretched, along with a part that is taken up by the angular acceleration of the pulley.

Suggestion is to write the forces $F$ on $m_p$, so that $F=m_p s''$ with tension $T=-ks-torque/r$, where $torque=dL/dt$, etc.

 

[lorenz0]

What about the pulley and its effect on the frequency? They should have given you a value for the mass of the pulley=call it $m_o$.

In addition, for part (3), I think the forces on $m_p$ are more complex than what you have. On $m_p$ you have the tension from the rope, and the force of gravity, i.e. the component along the incline. You then have the tension in the rope, (that is not the same everywhere), affected by how much the spring is stretched, along with a part that is taken up by the angular acceleration of the pulley.

From $\begin{cases}(ks-T)r=I_0 \alpha=\frac{I_0}{r}a\\ T-m_p g\sin(\alpha)=m_p a \end{cases}$ I get $a=-\frac{m_p}{m_p+\frac{I}{r^2}}g\sin(\alpha)+\frac{k}{m_p+\frac{I_0}{r^2}}s$ so $\omega=\sqrt{\frac{k}{m_p+\frac{I_0}{r^2}}}$ thus $T=\frac{2\pi}{\omega}=\frac{2\pi}{\sqrt{\frac{k}{m_p+\frac{I_0}{r^2}}}}$ but I am unsure about whether I have chosen the correct positive and negative signs of the various quantities.

 

[Charles Link]

Very good. :) Let $T$ be positive: $T=ks-I_o s''/r^2$ and $m_p g \sin{\alpha}-T=m_p s''$. I agree with your first expression, but I think the signs are incorrect on the second.
($s$ is positive to the right, down the incline).

Edit: We later determined the first expression should read $T=ks+I_o s''/r^2$. See posts 8 and 9 below.

 

[lorenz0]

Very good. :) Let $T$ be positive: $T=ks-I_o s''/r^2$ and $m_p g \sin{\alpha}-T=m_p s''$. I agree with your first expression, but I think the signs are incorrect on the second.

Thanks. So, $\begin{cases}(T-ks)r=I_0 (-\alpha)=-I_0\frac{a}{r}\\ m_p g\sin(\alpha)-T=m_p a\end{cases}\Rightarrow a=\frac{m_p}{m_p-\frac{I_0}{r^2}}g\sin(\alpha)-\frac{k}{m_p-\frac{I_0}{r^2}}s\Rightarrow \omega=\sqrt{\frac{k}{m_p-\frac{I_0}{r^2}}}\Rightarrow T=\frac{2\pi}{\omega}=\frac{2\pi}{\sqrt{\frac{k}{m_p-\frac{I_0}{r^2}}}}$: is this correct?

 

[Charles Link]

Try your algebra again: I get a plus sign on the $I_o/r^2$.

 

[lorenz0]

Try your algebra again: I get a plus sign on the $I_o/r^2$.

I had forgotten the $-$ sign on $\alpha$ in the first equation. With that, $a=\frac{m_p}{m_p-\frac{I_0}{r^2}}g\sin(\alpha)-\frac{k}{m_p-\frac{I_0}{r^2}}s$

 

[Charles Link]

My mistake=I believe the first expression should read $T=ks+I_o s''/r^2$. Then it should get the correct sign on $I_o$. Edit: Let me double-check that...

 

[Charles Link]

Yes, that is the problem. I think this error resulted because the tension $T$ in the very right segment of the rope between the pulley and the mass is peculiar in that it pulls the mass $m_p$ to the left, but it will pull the pulley to the right.

The tension $T$ is not a vector. From $T$ the force vector is determined, and it points in different directions for the two items. It points towards the rope in each case.

 

[Charles Link]

and be sure and see the last couple of sentences I added to the previous post.

 

[Charles Link]

To get the first expression with the correct signs, it helps to look at just the pulley and consider the rope(s) anchored to it with one rope pulling to the left with force $ks$ and the other pulling to the right with tension $T$. We then get $I_o s''/r^2=T-ks$, which agrees with post 8.