- #1
guyvsdcsniper
- 264
- 37
- Homework Statement
- Prove the I/E formula for 3 events by 1st applying
I/E to (A∪B) ∪Z. In other words, consider (A∪B) as a
single event "Y" and then apply I/E between "Y" and Z.
- Relevant Equations
- P(A∪B)=P(A)+P(B)−P(A∩B)
P(A∪B∪C)=P(A)+P(B)+P(C)−
−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)
Below is my attempt at the problem. I used the distributive law and applied to what was given, (A∪B)∪Z which equates to (A∪Z)∩(B∪Z). I then applied the 2 set I/E formula to each union. Since there is an intersection between these two sets I added them.
But I end up with 2 P(Z) which doesn't seem right.
I feel like I am got the distributive property part down but definitely getting something wrong past that.
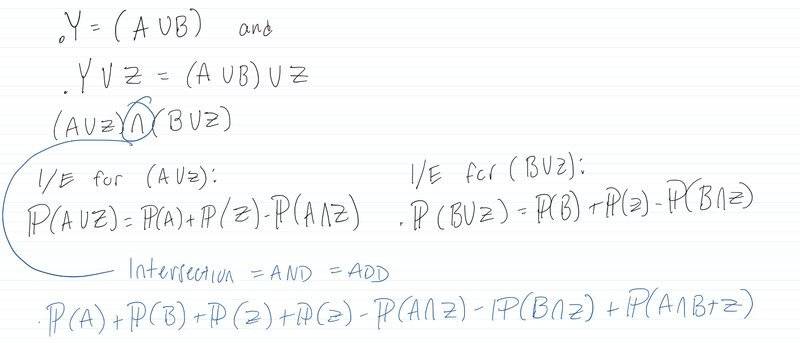
But I end up with 2 P(Z) which doesn't seem right.
I feel like I am got the distributive property part down but definitely getting something wrong past that.