Increase and decrease functions

[jose1]

Hello
I have tried to resolve an exercise which is asking how the graph is modified according to the variables into the function. I would appreciate any help since accordin to my udnerstanding the function should increase

Please, follow below:
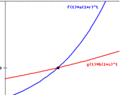
Suppose y0 is the y-coordinate of the point of intersection of the graphs below. Complete the statement below in order to correctly describe what happens to y0 if the value of a (in the blue graph of $$f(t)=a(1+r)t$$ below) is increased, and all other quantities remain the same.

If the value of a change, the function should be increased, but the answer is not. I would like to understand why?

View attachment 8577Regards,

Jose

 

[MarkFL]

Let's examine a live graph:

[DESMOS]advanced: {"version":5,"graph":{"viewport":{"xmin":-5.365861436977749,"ymin":-1.3327205737064363,"xmax":17.212263563022272,"ymax":7.291467737981876}},"expressions":{"list":[{"type":"expression","id":"graph1","color":"#2d70b3","latex":"y=1.25^t","style":"SOLID"},{"type":"expression","id":"2","color":"#388c46","latex":"y=a\\cdot1.5^t","style":"SOLID"},{"type":"expression","id":"3","color":"#fa7e19","latex":"a=1","hidden":true,"sliderHardMin":true,"sliderHardMax":true,"sliderMin":"0","sliderMax":"5","sliderInterval":".01","style":"SOLID"}]}}[/DESMOS]

Move the slider, and look at how the intersection point changes when you change \(a\)...