Piecewise Function: Intervals of Increase/Decrease & Extremes/Asymptotes

[Kolika28]

Homework Statement

$f(x)=\left\{ \begin{array}{ll} \frac{e^{-x}-1}{x}, & x>0 \\ \frac{x}{2}+1, & x\leq 0 \\ \end{array} \right.$

a) At which intervals are f strictly increasing and at what intervals are f strictly decreasing.
b) Determine any local and global extreme values for f.
c) Determines if f has asymptotes.

Relevant Equations

The derivative

a) At which intervals are f strictly increasing and at what intervals are f strictly decreasing.

Should I just find the derivative of both of the functions? If so, I get that the function is increasing at the intervals (−∞,0) and (0,∞). Is this right, or can I just say that the function is increasing at the interval (−∞,∞)?

b) Determine any local and global extreme values for f.

When graphing the function I don't see any local or global extreme values. f(x) consists of a straight line and curve with where f(x)=0 is not true. The whole function is not bounded, so I can't look at the values in the endpoints. But my teacher says there are extreme values. But how so?

c) Determines if f has asymptotes.

I know there is at least one horisontal asymptote, y=0, given the first function. Because

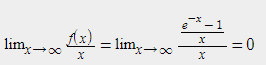
I was told there is one oblique asymptote also. But how?

 

[Orodruin]

a) You would just say that the function is strictly increasing everywhere.

b) The function is bounded from above, but it has no extreme points. (It has a supremum, but no maximal value.)

c) what happens for large negative x?

 

[Kolika28]

a) You would just say that the function is strictly increasing everywhere.

b) The function is bounded from above, but it has no extreme points. (It has a supremum, but no maximal value.)

c) what happens for large negative x?

b) Should I just say that it has a supremum then in x=0??
c) For large negative x I look at $\frac{x}{2}+1$. And I just get $-∞$ . But that does not tell me what the oblique slope is?

 

[LCKurtz]

a) You would just say that the function is strictly increasing everywhere.

Not on the interval [-1,1].

b) The function is bounded from above, but it has no extreme points. (It has a supremum, but no maximal value.)

$f(0) = 1$ is an absolute maximum.

 

[Orodruin]

Not on the interval [-1,1].
$f(0) = 1$ is an absolute maximum.

Oops. I just assumed OP had checked for continuity at x=0...

b) Should I just say that it has a supremum then in x=0??

No, it has a global max in x=0.

c) For large negative x I look at x2+1x2+1\frac{x}{2}+1. And I just get −∞−∞-∞ . But that does not tell me what the oblique slope is?

You are not looking for a value of the function. You are looking for a line on the form $kx+m$ that the function approaches.

 

[WWGD]

b) Should I just say that it has a supremum then in x=0??
c) For large negative x I look at $\frac{x}{2}+1$. And I just get $-∞$ . But that does not tell me what the oblique slope is?

The slope of a line is constant, here =1/2.

 

[Kolika28]

Ok, now I understand what you mean by task b. But I'm still confussed about c). So I'm supposed to find a line on the form $kx+m$.

You are not looking for a value of the function. You are looking for a line on the form kx+mkx+mkx+m that the function approaches.

The slope of a line is constant, here =1/2.

So is the oblique tanget just $\frac{x}{2}+1$?

 

[Kolika28]

Not on the interval [-1,1].

Hmm, why not this interval. Is the function decreasing here?

 

[Orodruin]

Hmm, why not this interval. Is the function decreasing here?

Not in the entire interval, no. You have (correctly) concluded that the function is increasing on (-infinity,0) and (0,infty). What is left to check?

 

[Kolika28]

Not in the entire interval, no. You have (correctly) concluded that the function is increasing on (-infinity,0) and (0,infty). What is left to check?

I'm sorry, but I'm really blank right now. I don't see what's left to check. Sorry, for all the questions by the way, I just really want to understand!

 

[Orodruin]

What is the value of f(0)? What is the value of f(0.000000001)?

 

[Kolika28]

What is the value of f(0)? What is the value of f(0.000000001)?

Ohh, I understand now. Thank you so much!My last question is:

So is the oblique tanget just x2+1x2+1\frac{x}{2}+1?