StoyanNikolov
- 50
- 0
- TL;DR
- inductive Reactance of Solenoid with Solid Metal Core With respect to frquency
Hi. Consider the Solenoid/Inductor Like one the Picture. There is Air gap between the coil and inserted solid metal.
Hi. Consider the Solenoid/Inductor Like one the Picture. There is Air gap between the coil and inserted solid metal. The solid metal is from Aluminum or Copper (Both have relative magnetic permeability , close to 1 regardless of temperature).
What will happen with inductive reactance of the given Solenoid if we increase the frequency of the applied voltage.
Thank you.
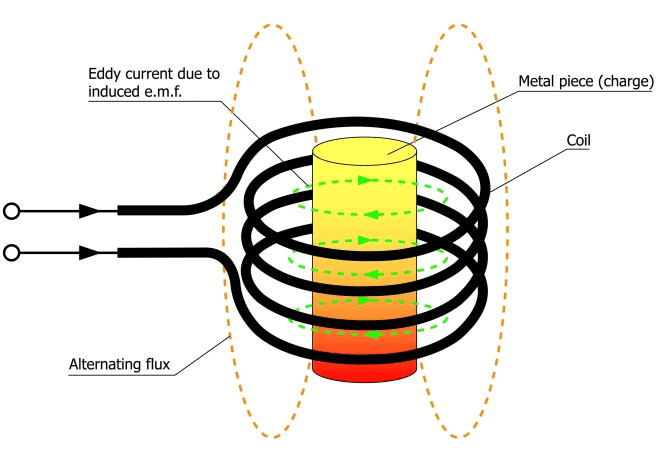
Hi. Consider the Solenoid/Inductor Like one the Picture. There is Air gap between the coil and inserted solid metal. The solid metal is from Aluminum or Copper (Both have relative magnetic permeability , close to 1 regardless of temperature).
What will happen with inductive reactance of the given Solenoid if we increase the frequency of the applied voltage.
Thank you.
Last edited: