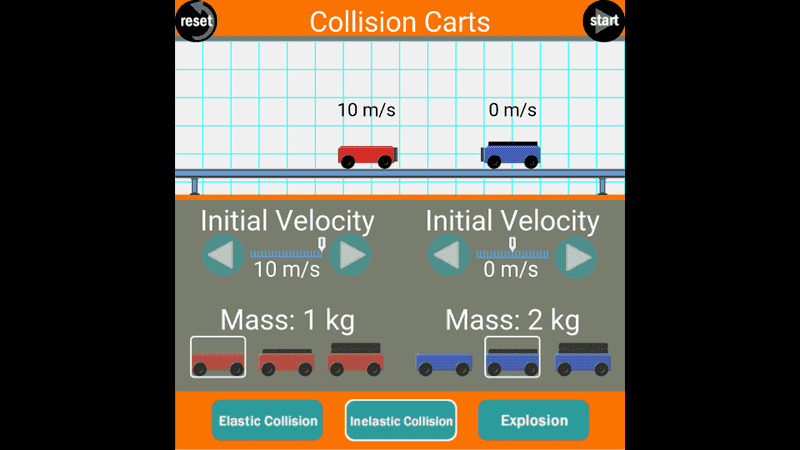
- #1
Karan Punjabi
- 127
- 3
Guys, I'm confused that how momentum is conserved when kinetic energy is lost?...I know this question is asked by many people and i searched for it but I'm not getting the reason. Here i have sent two photos which shows that momentum is not conserved from www.simbucket.com. If I am wrong at any point please correct me. Thankyou