I Inertial frames in changing gravitational fields

[bhobba]

When I teach GR I usually go by the EH action being the simplest non-trivial Lagrangian you can write down and ”oh look! you reproduce Newtonian gravity in the weak field non-relativistic limit and make a ton of other predictions that have been verified to high precision”.

That is an excellent way of doing it.

Thanks
Bill

 

[Android Neox]

The gravitational time dilation at any point in space is determined by the gravitational potential so, as a clock (or observer) moves downward, gravitational time dilation will increase and time will slow. The freely falling observer will have increasing time dilation (slower and slower time) both due to increasing speed (from the perspective of an observer stationary with respect to the massive body) and due to moving to space at lower gravitational potential.

 

[bhobba]

The freely falling observer will have increasing time dilation (slower and slower time) both due to increasing speed (from the perspective of an observer stationary with respect to the massive body) and due to moving to space at lower gravitational potential.

Is there a gravitational field for a freely falling observer?

I think I see what you are saying, but maybe it could be expressed a bit clearer.

Thanks
Bill

 

[Android Neox]

Is there a gravitational field for a freely falling observer?

I think I see what you are saying, but maybe it could be expressed a bit clearer.

Thanks
Bill

I should have been more clear.

No, all observations within the falling observer's frame and local to the observer (e.g. within a falling elevator) would not show any acceleration, gravitational or otherwise. Equivalence Principle holds. However, that's not the determining factor.

Since all correct models & thought experiments are correct (or, at least, not wrong) under all correct interpretations... a single correct thought experiment will yield observations that are logically consistent with those of all observers in all frames.

Thought experiment: Consider a platform, stationary with respect to a Schwarzschild black hole, at some finite coordinate distance above the Schwarzschild radius, $R_s$. On the platform is a winch that can lower a mirror. There is a laser that shines a beam onto the mirror. There is also a device that detects reflected laser light.

At any mirror position along the light beam, it will have some blueshift which follows, exactly, the difference in gravitational potential between the platform and the mirror. The change in time rate exactly follows this, too. If the frequency is doubled, the time rate is halved. That value of time dilation is an attribute of that frame. If the mirror is held stationary with respect to the black hole then that is the frame in which time passes at the maximum rate, for that point in space.

A freely falling observer will also have two other effects that will change the appearance of the light beam: Doppler and relativistic effects of motion with respect to the source.

If it's not clear that the change in laser beam frequency must be the exact inverse of the change in time rate, consider that every light wave cycle that reaches the mirror was first generated at the laser. The light beam is a causal sequence just as falling dominoes are, and so this sequence is the same for all observers in all frames. So, if a lower observer is seeing these wave cycles arriving at twice the rate, they must be measuring time half as fast.

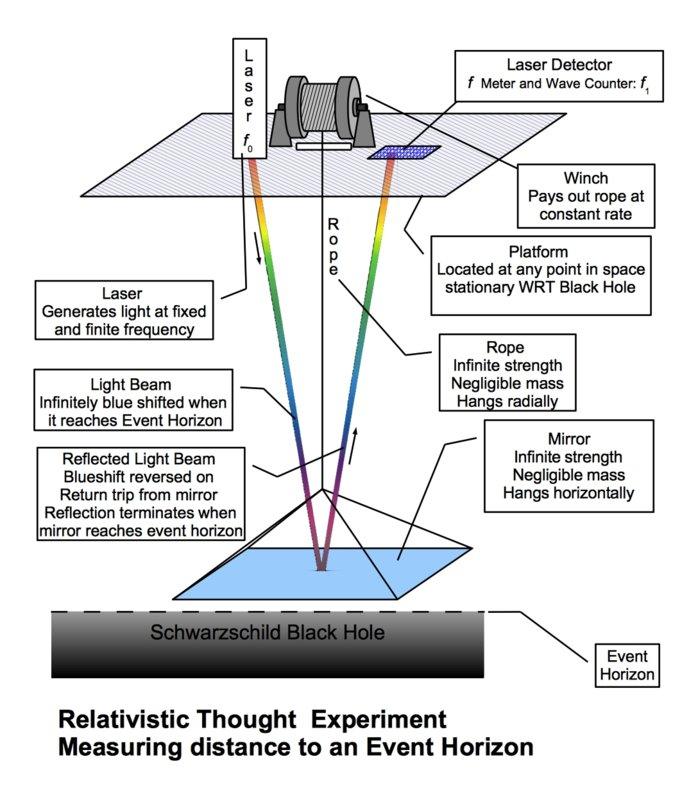
Because the blueshift down to an event horizon, from any point above the EH, is infinite, by the time the front of the beam reaches the event horizon, the beam will be infinitely blueshifted. The beam will contain infinitely many wave cycles. This means that, before the front of the beam can reach the event horizon, infinite time must pass for the light source on the platform. And, since the rope supporting the mirror has been payed out at a constant rate, an infinite amount of rope will be payed out before the front of the light beam could reach the event horizon. Since the mirror is lowered slower than c, it will take event longer than infinite time for the mirror to arrive.

Idealized: All equipment is of infinite strength, negligible mass, and otherwise idealized.

 

[PeterDonis]

at some finite coordinate distance above the Schwarzschild radius

In what coordinates? You appear to be implicitly using Schwarzschild coordinates in the patch exterior to the horizon, but you should not leave that implicit. You should state it explicitly. That way you will be forced to consider the limitations of the coordinates you are using; see further comments below.

At any mirror position along the light beam, it will have some blueshift

Measured by what?

If the mirror is held stationary with respect to the black hole then that is the frame in which time passes at the maximum rate, for that point in space.

"For that point in space" is ambiguous. If you mean "for objects held at that point in space" (and remember, to properly define "point in space" in a coordinate-independent fashion is not trivial, though in this case it can be done), then your statement is vacuous, since only one worldline--path through spacetime--is possible for any such object, and so only one possible rate of time passage is possible.

If, OTOH, you mean "for any objects whose worldlines pass through two selected events, chosen to be at that point in space", then your statement is false. If an observer held stationary along with the mirror throws a clock up in the air vertically, then catches it at some later time, the elapsed time on the clock he threw up will be greater than the elapsed time on the clock he carries with him.

If it's not clear that the change in laser beam frequency must be the exact inverse of the change in time rate

If you mean that the observed redshift/blueshift is exactly proportional to the ratio of gravitational potentials, of course it is. I don't see why you're making such a big deal out of it, since this is a well-known property of stationary observers in Schwarzschild spacetime and has been for decades.

Because the blueshift down to an event horizon, from any point above the EH, is infinite,

Wrong. There are no stationary observers at the EH, nor is it possible to hold the mirror stationary there. So there is no such thing as "the blueshift down to an event horizon", since it's impossible for an observer to exist who could measure it.

before the front of the beam can reach the event horizon, infinite time must pass for the light source on the platform

Wrong. The coordinates you appear to be implicitly using are singular at the horizon, so "infinite time must pass" is not correct because it is attempting to apply coordinates at a coordinate singularity.

since the rope supporting the mirror has been payed out at a constant rate, an infinite amount of rope will be payed out before the front of the light beam could reach the event horizon

Wrong. The proper distance from your laser platform to the mirror, as the mirror gets lowered, approaches a finite limit as the mirror approaches the horizon. (We cannot directly measure such a distance with the mirror at the horizon, since the mirror can't be stationary there, but we can realize the limiting process I have just described by letting the mirror get closer and closer and measuring how the distance varies.)

It looks like you need to read the Insights series on the Schwarzschild geometry:

https://www.physicsforums.com/insights/schwarzschild-geometry-part-1/

You are making a number of elementary errors that are common with people who are not sufficiently familiar with the actual properties of this spacetime geometry.

 

[Android Neox]

It looks like you need to read the Insights series on the Schwarzschild geometry:

https://www.physicsforums.com/insights/schwarzschild-geometry-part-1/

You are making a number of elementary errors that are common with people who are not sufficiently familiar with the actual properties of this spacetime geometry.

Thanks for the response. I'll do that.
I'll probably be back, later, with some new misinterpretations.

 

[bhobba]

I'll probably be back, later, with some new misinterpretations.

Don't worry - that's how you learn.

Thanks
Bill