- #1
DRose87
- 10
- 0
(Not an assigned problem...)
1. Homework Statement
pg 244 of "Mathematical Methods for Physics and Engineering" by Riley and Hobson says that given the following two properties of the inner product
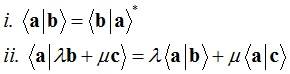
It follows that:
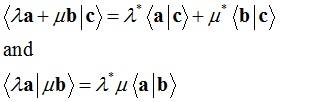
2. Attempt at a solution.
I think that both of these solutions are valid...but even if they are valid, is there a simpler and more intuitive way to derive these properties of inner products for a complex vector space from i and ii?
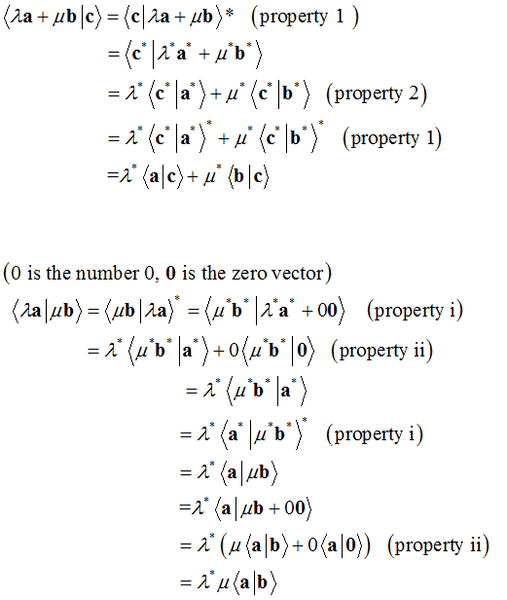
1. Homework Statement
pg 244 of "Mathematical Methods for Physics and Engineering" by Riley and Hobson says that given the following two properties of the inner product
It follows that:
2. Attempt at a solution.
I think that both of these solutions are valid...but even if they are valid, is there a simpler and more intuitive way to derive these properties of inner products for a complex vector space from i and ii?