Integral Calculation with Complex Analysis - Can Residue Theorem Help?

[asi123]

Hey guys.
I need to calculate this integral so I was thinking about using the residue theorem.
The thing is that the point 0 is not enclosed within the curve that I'm about to build, it's on it.
Can I still use the theorem?

Thanks a lot.

 

[MathematicalPhysicist]

So use Cauchy Principal value to bypass the singularity at 0.

 

[lurflurf]

You have a bigger problem then that, the residue at x=0 is zero (removeable singularity). This is a standard example and is often done as follows
consider
To fix the residue=0 problem add in an odd function the usual one is to use
exp(x i)/x=cos(x)/x+i sin(x)/x
the cos(x)/x diverges as an improper integral, but as lqg states cauch principle sense may be used
now consider ther contour formed by theese pieces
(-R,r) straight line
(-r,r) semicircle arc about z=0
(r, R) straight line
(R,r) semicircle arc about x=0

 

[asi123]

You have a bigger problem then that, the residue at x=0 is zero (removeable singularity). This is a standard example and is often done as follows
consider
To fix the residue=0 problem add in an odd function the usual one is to use
exp(x i)/x=cos(x)/x+i sin(x)/x
the cos(x)/x diverges as an improper integral, but as lqg states cauch principle sense may be used
now consider ther contour formed by theese pieces
(-R,r) straight line
(-r,r) semicircle arc about z=0
(r, R) straight line
(R,r) semicircle arc about x=0

I didn't quite understand the contour you described there.
What's R and What's r?

Thanks a lot.

 

[lurflurf]

I didn't quite understand the contour you described there.
What's R and What's r?

Thanks a lot.

Take limits R-> +infinity,r->+0
If you draw a pictuis an upper semicircle that in the limit is large with a tiny semicircle at the origin then you get for the various integrals

(-R,r) straight line
-infinity+(Integral you want)/2
(-r,r) semicircle arc about z=0
{+,-}[+ if it was upper - if it was lower] pi*i (residue theorem)
(r, R) straight line
-infinity+(integral you want)/2
(R,r) semicircle arc about x=0
0

 

[asi123]

Take limits R-> +infinity,r->+0
If you draw a pictuis an upper semicircle that in the limit is large with a tiny semicircle at the origin then you get for the various integrals

(-R,r) straight line
-infinity+(Integral you want)/2
(-r,r) semicircle arc about z=0
{+,-}[+ if it was upper - if it was lower] pi*i (residue theorem)
(r, R) straight line
-infinity+(integral you want)/2
(R,r) semicircle arc about x=0
0

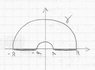
Is it something like that?

Thanks again.

 

[lurflurf]

Is it something like that?

Thanks again.

That is it. I guess that is one reasone why some people do not like old math books with no pictures. Were you able to finish?

 

[asi123]

That is it. I guess that is one reasone why some people do not like old math books with no pictures. Were you able to finish?

I'll try, if I'll have some troubles, I'll be back .
Thanks a lot.