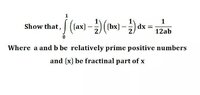Divide the unit interval into $ab$ subintervals $\bigl[\frac r{ab},\,\frac{r+1}{ab}\bigr]$ of length $\frac1{ab}$, for $0\leqslant r <ab.$ In each subinterval, $x = \frac r{ab} + t$ (where $0\leqslant t\leqslant \frac1{ab}$), and $ax = \frac rb + at$. Thus $\{ax\} = \bigl\{ \frac rb \bigr\} + at = \frac kb + at$ for some $k$ with $0\leqslant k <b.$ Similarly, $\{bx\} = \bigl\{ \frac ra \bigr\} + bt = \frac la + bt$ for some $l$ with $0\leqslant l <a.$
You then need to show that as $r$ goes from $0$ to $ab-1$, each of the possible values of the pair $k,\: l$ (with $0\leqslant k <b,\ 0\leqslant l <a$) occurs exactly once. To prove that, you will need to use the fact that $a$ and $b$ are relatively prime.
It will then follow that $$\begin{aligned} \int_0^1\bigl(\{ax\} - \tfrac12\bigr) \bigl(\{bx\} - \tfrac12\bigr) &= \sum_{k=0}^{b-1} \sum_{l=0}^{a-1} \int_0^{1/(ab)} \bigl(at + \tfrac kb -\tfrac12\bigr) \bigl(bt + \tfrac la -\tfrac12\bigr) dt \\ &=\int_0^{1/(ab)} \sum_{k=0}^{b-1}\bigl(at + \tfrac kb -\tfrac12\bigr) \sum_{l=0}^{a-1}\bigl(bt + \tfrac la -\tfrac12\bigr) dt \\ &= \int_0^{1/(ab)} \bigl(abt + \tfrac 12(b-1) -\tfrac12b\bigr) \bigl(abt + \tfrac 12(a-1) -\tfrac12a\bigr)dt \\ &= \int_0^{1/(ab)} \bigl(abt - \tfrac 12\bigr)^2dt \\ &= \Bigl[\tfrac1{3ab}\bigl(abt - \tfrac 12\bigr)^3 \Bigr]_0^{1/(ab)} \\ &= \tfrac1{3ab} \bigl(\tfrac18 + \tfrac18\bigr) = \tfrac1{12ab}. \end{aligned}$$