Integrating to find the volume of sphere

[mimi.janson]

Homework Statement

Hi I have a question about integrating to find the volume of a sphere but before that i need to tell all other results i got or it will not make sence.

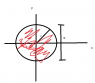
1. I needed to show how you get the formula for finding the volume of a sphere by the help of a cirkle with radius r . I used the rule "The volume of the solid formed by rotating the area between the curves of f(x) and g(x)"

I solved it by integrating and got the result volume =4/3 π*r³

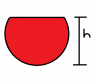
2. I had to find the volume if the height h i from 0 to 2r. (which means the whole sphere)
I know the result is (π/6)*h*(3*a²+h²), because the formula was in my book. But i need to use the same rule of rotating the area around the x axsis, but i don't know how i can do it that way?

3. I had to find the radius if v is 2500. here i just put the v into the formula and isolated r which i got to be 8,4

Besides that i need to show a graph of V as the function of h which i don't know how i can

Homework Equations

1. relevant formula v=(4/3)*π*r³
2. relevant formulav=(π/6)*h*(3*a²+h²)

The Attempt at a Solution

i attemted to find the solution for nr.2 by integrating √r²-x² since that is the normal ecuation for a circle.

y=f(x)=∏∫ from 0 to 2r (√r²-x² )^2 dx where i tried to make it shorter by trying to get rid of the ^2

but when i did i got (√r²-x² )-(√r²-x² ) and to be honest i feel quite a bit lost in this

for showing the graph i have to say that v(h) is on the y-axis and h is on the x-axis but i don't get what is v(h) and how to find h alone in this

please i would be gratefull for some help

 

[BruceW]

hmm. So you've already used rotation of the circle around the x-axis to get the full volume of the sphere. But now, the problem is that they want you to integrate only only up to a certain height, so the top of the sphere is going to get cut off, right? (I attached a picture of what I think it looks like, tell me if I've not got it right). So anyway, you need to find the area of this shape, then use rotation of that around the x-axis to get the volume of the object.

So to begin with, you need to find the 2d area of a 'cut-off circle'. You don't need to think about volumes straight away. It still takes a bit of work to find the area of a 'cut-off circle' (If you haven't memorised the equation for it). And I should use the correct terminology, sorry. I think the bit being cut-off is called a circle segment, to use the proper word :) Anyway, I think there are a few ways to solve for it. Are you familiar with polar coordinates?