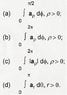Integration in cylindrical coordinates

[╔(σ_σ)╝]

Homework Statement

In cyclindrical coordinates we can represent points as ($$\rho$$,$$\phi$$,z)

We define a vector in cyclindrical coordinates as follows

A = A$$\rho$$a$$\rho$$ + A$$\phi$$a$$\phi$$ + A_za_z

I'm having some problem with subscripts.

Anyway I don't understand this.

If I am given a point say ( 5, 20 deg, 4)

Without writing

x = $$\rho$$cos$$\phi$$
y = $$\rho$$sin$$\phi$$

And then transforming to back to cylindrical coordinates...

How can I determine A$$\rho$$, A$$\phi$$
And my prof gave us a review question for vector calculus but I don't seem to understand the question geometrically.

It says $$\int$$a$$\rho$$d$$\phi$$ from 0 to pi/2

having a bit of trouble with the latex.

Anyway the function in the integral is the unit vector a$$\rho$$

Homework Equations

The Attempt at a Solution

I just need to understand what the integral is asking for in other to attempt it. I'm having some trouble working with cylindrical coordinates in the way it's defined in my field theory book.

 

[Dick]

Sorry, but neither of these questions really make a lot of sense. E.g. for the second one you need to integrate a vector along a definite path in the coordinate space. Just saying phi goes from 0 to pi/2 doesn't define a path. Unlike in cartesian coordinates the value of a_rho depends on where you are. I'm hopeless confused.

 

[╔(σ_σ)╝]

Sorry, but neither of these questions really make a lot of sense. E.g. for the second one you need to integrate a vector along a definite path in the coordinate space. Just saying phi goes from 0 to pi/2 doesn't define a path. Unlike in cartesian coordinates the value of a_rho depends on where you are. I'm hopeless confused.

Well this is the integral we were given to evaluate. I am also hopelessly confused which is why I'm asking the question.

I provided images if they help . Can you just point me in the right direction if you can!Or can you direct me to a book with gives a through consideration of cylindrical Coordinates my book is a piece of crap and my multivarible cal book did not cover cylindrical in this manner it was more straight forward in it's approach.

 

[Dick]

Ok. Maybe they mean you convert the vector to Cartesian coordinates and then just integrate? a_rho=(cos(phi),sin(phi),0). Just integrate component by component. The result will an Cartesian vector if the integrand is a vector - a scalar if it's not.

 

[tiny-tim]

HI ╔(σ_σ)╝!

(have a rho: ρ and a phi: φ and a degree: º and an integral: ∫ and type "itex" instead of "tex" to get the LaTeX in-line )

If I am given a point say ( 5, 20 deg, 4)
…
How can I determine A$$\rho$$, A$$\phi$$

You need two points for a vector.

The vectors in your questions do not start from the origin, they start from eg (5, 20º, 4).

a_φ etc are different unit vectors at each point.

To evaluate eg ∫₀^π/2 a_ρ dφ,

you go round the curve (you haven't said what it is … is it a circle of radius ρ? ), integrating the different "radial" unit vector a_ρ for each point on the curve.

 

[╔(σ_σ)╝]

Ok. Maybe they mean you convert the vector to Cartesian coordinates and then just integrate? a_rho=(cos(phi),sin(phi),0). Just integrate component by component. The result will an Cartesian vector if the integrand is a vector - a scalar if it's not.

Okay thanks. I don't know why the prof defined the integral is such a way. My next question is what is the interpretation of this integral ? The area under what ?

dφ and a_ρ are orthogonal to each other because dφ is in the same direction as a_φ

HI ╔(σ_σ)╝!

(have a rho: ρ and a phi: φ and a degree: º and an integral: ∫ and type "itex" instead of "tex" to get the LaTeX in-line )You need two points for a vector.

The vectors in your questions do not start from the origin, they start from eg (5, 20º, 4).

a_φ etc are different unit vectors at each point.

To evaluate eg ∫₀^π/2 a_ρ dφ,

you go round the curve (you haven't said what it is … is it a circle of radius ρ? ), integrating the different "radial" unit vector a_ρ for each point on the curve.

okay I understand what you mean. What about if I have two points say (5,45º,2) and (4,25º, 1) without using the equations:

x= pcosφ
y = psinφ

To find the cartisian equivalent how can I determine
$$A\upshape\rho$$ and $$A\upshape\phi$$ to present the vector from (4,25º, 1) to (5,45º,2) in the form

A_ρa_ρ+ A_φa_φ + A_za_z.

I am aware that to represent a position vector only two unit vectors are needed namely,a_ρand a_z because the unit vector a_ρ depends on the position of the unit vector a_φ

As for the integration my real question is what exactly does this integrand mean... I mean we intepret an integral as the area under a curve but how can I interpret this ?

I understand that depending on the angle $$\phi$$ the oriendtation of the unit vector a_φchanges which in turn change a_ρ because they are mutually orthogonal.

 

[tiny-tim]

… what is the interpretation of this integral ? The area under what ?
…

As for the integration my real question is what exactly does this integrand mean... I mean we intepret an integral as the area under a curve but how can I interpret this ?

An integral only works as an area if all the vectors are in the same direction.

a_ρ, for example, keeps changing direction.

There isn't really a geometrical way of understanding a vector integral along a curve (though I suppose you could imagine all the a_ρs being moved to the same point, and then added together vectorially).

I am aware that to represent a position vector only two unit vectors are needed namely,a_ρand a_z because the unit vector a_ρ depends on the position of the unit vector a_φ

Sorry, I don't really understand that, but it's wrong anyway …

you always need three unit vectors to specify a position vector in a 3D space.

What about if I have two points say (5,45º,2) and (4,25º, 1) without using the equations:

x= pcosφ
y = psinφ

To find the cartisian equivalent how can I determine
$$A\upshape\rho$$ and $$A\upshape\phi$$ to present the vector from (4,25º, 1) to (5,45º,2) in the form

A_ρa_ρ+ A_φa_φ + A_za_z.

You have to choose where the vector is "anchored" … if it's anchored at the first point, you use the unit vectors of that first point, and express the vector in components of those unit vectors.

 

[╔(σ_σ)╝]

Sorry, I don't really understand that, but it's wrong anyway …

you always need three unit vectors to specify a position vector in a 3D space.

Yes you are right I was referring to something else but that is of little importance.

You have to choose where the vector is "anchored" … if it's anchored at the first point, you use the unit vectors of that first point, and express the vector in components of those unit vectors.

Can you perhaps elaborate a bit more ? Perhaps an example ?

I'm not sure what you mean by "use the unit vectors of that first point, and express the vector in components of those unit vectors".

An quick example would be highly appreciated because I always convert back to cartesian find the position vector and then back to cylindrical coordinates which is a daunting and involving task .

 

[tiny-tim]

I'm not sure what you mean by "use the unit vectors of that first point, and express the vector in components of those unit vectors".

The three unit vectors at one point form an i j k frame.

You have to write the vector as ai + bj + ck.

(You do not "convert back" to cylindrical coordinates, you leave it like that.)

 

[vela]

okay I understand what you mean. What about if I have two points, say (5, 45º, 2) and (4, 25º, 1), without using the equations:

x=pcosφ
y=psinφ

To find the cartesian equivalent, how can I determine $$A_\rho$$ and $$A_\phi$$ to present the vector from (4, 25º, 1) to (5, 45º,2) in the form

$$A_\rho{a_\rho}+A_\phi{a_\phi}+A_z{a_z}$$.

Perhaps a simpler example would help. Suppose you have the vector $$\vec{v}=(v_x,v_y,v_z)=(1,2,3)$$ located at the point $$\vec{x}=(x,y,z)=(0,4,0)$$. The point $$\vec{x}$$ is represented in cylindrical coordinates as $$(r,\phi,z)=(4, \pi/2, 0)$$, and the three cylindrical unit vectors for that point, represented in Cartesian coordinates, would be

$$\hat{a}_\rho = (0,1,0)$$
$$\hat{a}_\phi = (-1,0,0)$$
$$\hat{a}_z = (0,0,1)$$

The representation of the vector $$\vec{v}$$ in cylindrical coordinates would be given by

$$A_\rho = \vec{v}\cdot\hat{a}_\rho = 2$$
$$A_\phi = \vec{v}\cdot\hat{a}_\phi = -1$$
$$A_z = \vec{v}\cdot\hat{a}_z = 3$$

or $$\vec{v}=2 \hat{a}_\rho - \hat{a}_\phi + 3 \hat{a}_z$$.

Suppose instead that the $$\vec{v}$$ was anchored at the point $$\vec{y}=(1,1,0)$$, which in cylindrical coordinates is $$(\sqrt{2},\pi/4,0)$$. This time you'd have

$$\hat{a}_\rho = (1/\sqrt{2},1/\sqrt{2},0)$$
$$\hat{a}_\phi = (-1/\sqrt{2},1/\sqrt{2},0)$$
$$\hat{a}_z = (0,0,1)$$

and

$$A_\rho = \vec{v}\cdot\hat{a}_\rho = 3/\sqrt{2}$$
$$A_\phi = \vec{v}\cdot\hat{a}_\phi = 1/\sqrt{2}$$
$$A_z = \vec{v}\cdot\hat{a}_z = 3$$.

 

[╔(σ_σ)╝]

The three unit vectors at one point form an i j k frame.

You have to write the vector as ai + bj + ck.

(You do not "convert back" to cylindrical coordinates, you leave it like that.)

Thanks for all your help thus far ! It's highly appreciated.

I think I understand what you are getting at, with the help of vela example. :D

Perhaps a simpler example would help. Suppose you have the vector $$\vec{v}=(v_x,v_y,v_z)=(1,2,3)$$ located at the point $$\vec{x}=(x,y,z)=(0,4,0)$$. The point $$\vec{x}$$ is represented in cylindrical coordinates as $$(r,\phi,z)=(4, \pi/2, 0)$$, and the three cylindrical unit vectors for that point, represented in Cartesian coordinates, would be

$$\hat{a}_\rho = (0,1,0)$$
$$\hat{a}_\phi = (-1,0,0)$$
$$\hat{a}_z = (0,0,1)$$

The representation of the vector $$\vec{v}$$ in cylindrical coordinates would be given by

$$A_\rho = \vec{v}\cdot\hat{a}_\rho = 2$$
$$A_\phi = \vec{v}\cdot\hat{a}_\phi = -1$$
$$A_z = \vec{v}\cdot\hat{a}_z = 3$$

or $$\vec{v}=2 \hat{a}_\rho - \hat{a}_\phi + 3 \hat{a}_z$$.

Suppose instead that the $$\vec{v}$$ was anchored at the point $$\vec{y}=(1,1,0)$$, which in cylindrical coordinates is $$(\sqrt{2},\pi/4,0)$$. This time you'd have

$$\hat{a}_\rho = (1/\sqrt{2},1/\sqrt{2},0)$$
$$\hat{a}_\phi = (-1/\sqrt{2},1/\sqrt{2},0)$$
$$\hat{a}_z = (0,0,1)$$

and

$$A_\rho = \vec{v}\cdot\hat{a}_\rho = 3/\sqrt{2}$$
$$A_\phi = \vec{v}\cdot\hat{a}_\phi = 1/\sqrt{2}$$
$$A_z = \vec{v}\cdot\hat{a}_z = 3$$.

Okay I see , it's pretty much using the transformation matrix... perfect.

So you represent the point using the coordintes of the initial point. Besically you fix your coordinate system to make it stationary.

Thanks a lot.