Vector calculus: line element dr in cylindrical coordinates

[chiyu]

We were taught that in cylindrical coodrinates, the position vector can be expressed as

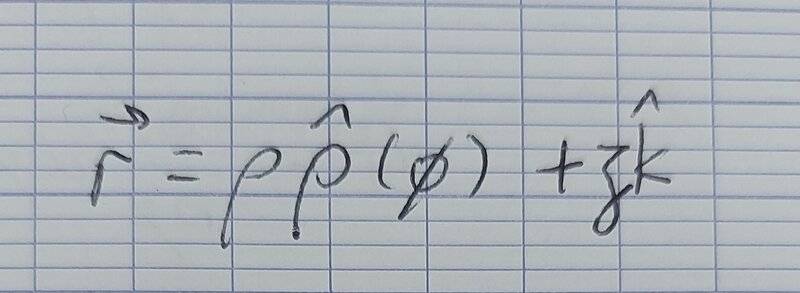
And then we can write the line element by differentiating to get

.

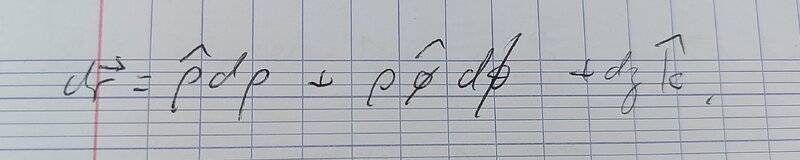We can then use this to do a line integral with a vector field along any path. And this seems to be what is done on all questions I've seen.However, if we are given the equations of the path, and it say rho is dependant on the other coordinates, wouldn't that change what dr is? For example:

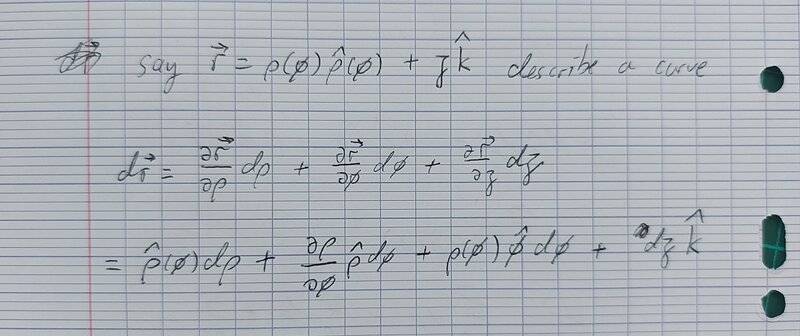
Wouldn't this be the right equation? Or am I misunderstanding something?

 

[kuruman]

Think of $d\vec r$ as a directed length element in space. It has components in three mutually perpendicular direction defined by the three unit vectors in cylindrical coordinates.

• In the radial direction the component is a radial element of length $d\rho$.
• In the azimuthal direction the component is an arc element of length $\rho~d\phi$.
• In the axial direction the component is an axial element of length $dz$.

So putting these components together to form a directed element, you get
$d\vec{r}=d\rho~\hat{\rho}+\rho~d\phi~\hat{\phi}+dz~\hat z.$
Knowing this, you can construct the volume element in cylindrical coordinates as the procuct of the three "sides", $dV=\rho~d\rho~ d\phi~ dz.$ An area element parallel to the $xy$-plane is $dA=\rho~d\rho~ d\phi$ and so on.

 

[pasmith]

The factor of $\rho$ can also be deduced on dimensional grounds: $d\rho$ and $dz$ are lengths, but $d\phi$ is dimensionless (an angle).

Also, the unit vectors $e_\rho$ and $e_\phi$ are not constant, but depend on $\phi$. Hence $$\begin{split} \frac{\partial \mathbf{F}}{\partial \phi} &= \frac{\partial F_r}{\partial \phi}e_r + F_r\frac{\partial e_r}{\partial \phi} + \frac{\partial F_\phi}{\partial \phi} e_\phi + F_\phi \frac{\partial e_\phi}{\partial \phi} + \frac{\partial F_z}{\partial \phi} e_z \\ &= \left(\frac{\partial F_r}{\partial \phi} - F_\phi\right)e_r + \left(F_r + \frac{\partial F_\phi}{\partial \phi}\right)e_\phi + \frac{\partial F_z}{\partial \phi}e_z.\end{split}$$

 

[kuruman]

The factor of $\rho$ can also be deduced on dimensional grounds: $d\rho$ and $dz$ are lengths, but $d\phi$ is dimensionless (an angle).

That is true. However @chiyu's expression has an additional term $\dfrac{\partial\rho}{\partial \phi}\hat{\rho}~d\phi$ which is dimensionally correct but does not belong. Of course, one can always argue that this term is zero because $\rho$ by definition does not explicitly depend on $\phi$, but why complicate matters?

 

[vanhees71]

The easiest way is to express the Cartesian coordinates in terms of the cylinder coordinates,
$$\vec{x}=\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}=\begin{pmatrix} \rho \cos \varphi \\ \rho \sin \varphi \\ z \end{pmatrix}.$$
Then
$$\mathrm{d} \vec{x} = \mathrm{d} \rho \begin{pmatrix}\cos \varphi \\ \sin \varphi \\ 0 \end{pmatrix} + \mathrm{d} \varphi \rho \begin{pmatrix}-\sin \varphi \\ \cos \varphi \\ 0 \end{pmatrix} + \mathrm{d} z \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}.$$
It's easy to see that the three column vectors appearing in this equation form a Cartesian bases and thus
$$\mathrm{d} \vec{r}^2 = \mathrm{d} \rho^2 + \rho^2 \mathrm{d} \varphi^2 +\mathrm{d} z^2.$$

 

[chiyu]

That is true. However @chiyu's expression has an additional term $\dfrac{\partial\rho}{\partial \phi}\hat{\rho}~d\phi$ which is dimensionally correct but does not belong. Of course, one can always argue that this term is zero because $\rho$ by definition does not explicitly depend on $\phi$, but why complicate matters?

Hey thanks for your help. I am a bit confused about why $\rho$ doesn't depend on $\phi$? I get that that is the case for a position vector to any point in space, but if the curve we defined has $\rho$ as a function of $\phi$, why would it still be the case that the additional term is 0?

 

[kuruman]

Hey thanks for your help. I am a bit confused about why $\rho$ doesn't depend on $\phi$? I get that that is the case for a position vector to any point in space, but if the curve we defined has $\rho$ as a function of $\phi$, why would it still be the case that the additional term is 0?

$\rho$ is the distance (a scalar) and does not depend on. Imagine a circle of radius $\rho$. It is the same regardless of the angle relative to a Cartesian coordinate system.
$\hat {\rho}$ is a unit vector and does depend on the angle relative to a Cartesian coordinate system.

Consider a point in the xy-plane. In Cartesian coordinates you write its position vector as
$\vec r=x~\hat x+y~\hat y.$
In cylindrical coordinates the same position vector is
$\vec r=\rho~\hat \rho.$
You can connect the two by noting that $x=\rho\cos\!\phi$ and $y=\rho\sin\!\phi.$ Then
$\vec r=\rho\cos\!\phi~\hat x+\rho\sin\!\phi~\hat y=\rho(\cos\!\phi~\hat x+\sin\!\phi~\hat y)=\rho~\hat \rho.$
It follows that $\hat \rho=(\cos\!\phi~\hat x+\sin\!\phi~\hat y)$
Clearly, it's the unit vector $\hat \rho$ that depends on the angle not the coordinate $\rho$.

 

[chiyu]

$\rho$ is the distance (a scalar) and does not depend on. Imagine a circle of radius $\rho$. It is the same regardless of the angle relative to a Cartesian coordinate system.
$\hat {\rho}$ is a unit vector and does depend on the angle relative to a Cartesian coordinate system.

Consider a point in the xy-plane. In Cartesian coordinates you write its position vector as
$\vec r=x~\hat x+y~\hat y.$
In cylindrical coordinates the same position vector is
$\vec r=\rho~\hat \rho.$
You can connect the two by noting that $x=\rho\cos\!\phi$ and $y=\rho\sin\!\phi.$ Then
$\vec r=\rho\cos\!\phi~\hat x+\rho\sin\!\phi~\hat y=\rho(\cos\!\phi~\hat x+\sin\!\phi~\hat y)=\rho~\hat \rho.$
It follows that $\hat \rho=(\cos\!\phi~\hat x+\sin\!\phi~\hat y)$
Clearly, it's the unit vector $\hat \rho$ that depends on the angle not the coordinate $\rho$.

But let's say instead of a circle, we take the surface of a oblong cylinder, then depending on the angle the distance will change right?

 

[kuruman]

But let's say instead of a circle, we take the surface of a oblong cylinder, then depending on the angle the distance will change right?

You are confusing the general expression of a directed element $d\mathbf{ r}$ with a specific directed element subject to constraints for doing a specific line integral. Let me show you what I mean. Say you have a vector field $$\mathbf{E}=E_{\rho}(\rho,\phi,z)\hat {\rho}+E_{\phi}(\rho,\phi,z)\hat {\phi}+E_z(\rho,\phi,z)\hat {z}.$$In this expression, coordinates $\rho$, $\phi$ and $z$ are placeholders for any radial distance $\rho$, any polar angle $\phi$ and any axial distance $z$. They are completely independent of each other and the field doesn't give a hoot whether you want to do a line integral along a circle or an ellipse or a squiggle. It is what it is. Likewise the directed element $d\mathbf{r}$ is, as has already been said, is always $$d\mathbf{r}=d\rho~\hat{\rho}+\rho~d\phi~\hat{\phi}+dz~\hat z.$$It follows that the integrand of a line integral in cylindrical coordinates is $$\begin{align}\mathbf{E}\cdot d\mathbf{r} & =[E_{\rho}(\rho,\phi,z)\hat {\rho}+E_{\phi}(\rho,\phi,z)\hat {\phi}+E_z(\rho,\phi,z)\hat {z}]\cdot (d\rho~\hat{\rho}+\rho~d\phi~\hat{\phi}+dz~\hat z)\nonumber \\
&= E_{\rho}(\rho,\phi,z)d\rho+E_{\phi}(\rho,\phi,z)\rho~d\phi+E_z(\rho,\phi,z)dz \nonumber \\
\end{align}.$$The above expression is always the integrand of a line integral regardless of the shape of the line you are integrating over. I repeat once more that $r$, $\phi$ and $z$ are independent coordinates which means that the partial derivative of one with respect to another is zero.

Now how do you set up a specific line integral? Say you want to do a line integral in the xy-plane along a circle of radius $R$ from $\phi_1$ to $\phi_2$. The equation of a circle in cylindrical coordinates in the xy-plane is $\rho=R$, $d\rho=0$ and $z=dz=0.$ With these replacements, the integrand becomes
$$\mathbf{E}\cdot d\mathbf{r} = E_{\phi}(R,\phi,0)R~d\phi$$and you have to integrate from $\phi_1$ to $\phi_2.$

Now say you want to do a line integral along an ellipse of semi-major axis $a$ and eccentricity $e$. The equation of this ellipse in cylindrical coordinates in the xy plane is $$\rho(\phi)=\frac{a(1-e^2)}{1+e\cos\phi}\implies d\rho=\frac{ae(1-e^2)\sin\phi}{(1+e\cos\phi)^2}d\phi$$ and, of course $z=dz=0.$ Then $$\mathbf{E}\cdot d\mathbf{r}=E_{\rho}(\rho(\phi),\phi,0)\frac{ae(1-e^2)\sin\phi}{(1+e\cos\phi)^2}d\phi+E_{\phi}(\rho(\phi),\phi,0)\rho(\phi)~d\phi$$and you have to integrate from $\phi_1$ to $\phi_2.$
To summarize, the general expression for a directed element is
$$d\mathbf{r}=d\rho~\hat{\rho}+\rho~d\phi~\hat{\phi}+dz~\hat z.$$ The specific directed element along a circle in the xy-plane is $$d\mathbf{r}=\rho~d\phi~\hat{\phi}.$$The specific directed element along an ellipse in the xy-plane is $$d\mathbf{r}=\frac{a(1-e^2)}{1+e\cos\phi}\left[\frac{e\sin\phi}{(1+e\cos\phi)}~\hat{\rho}+\hat{\phi}\right]d\phi.$$Do you see how it works?

 

[chiyu]

To summarize, the general expression for a directed element is
$$d\mathbf{r}=d\rho~\hat{\rho}+\rho~d\phi~\hat{\phi}+dz~\hat z.$$ The specific directed element along a circle in the xy-plane is $$d\mathbf{r}=\rho~d\phi~\hat{\phi}.$$The specific directed element along an ellipse in the xy-plane is $$d\mathbf{r}=\frac{a(1-e^2)}{1+e\cos\phi}\left[\frac{e\sin\phi}{(1+e\cos\phi)}~\hat{\rho}+\hat{\phi}\right]d\phi.$$Do you see how it works?

Ah I think I do now! Am I right in saying then that $$d\mathbf{r}=d\rho~\hat{\rho}+\rho~d\phi~\hat{\phi}+dz~\hat z$$ is the general expression, and if in the specific case where $\rho$ depend on $\phi$, we can write $d\rho$ as $\frac{\partial \rho}{\partial \phi} d\phi$, so that will still get us with a line integral of only $d\phi$ in our example?

Also, I see why the general expression is right now, but I still don't think I quite understand why the second expression of $dr$ I wrote in the original images was wrong, as in, what's wrong in the reasoning to get there if we started with a $\rho$ that depends on $\phi$, and differentiated it?

 

[kuruman]

Also, I see why the general expression is right now, but I still don't think I quite understand why the second expression of $dr$ I wrote in the original images was wrong, as in, what's wrong in the reasoning to get there if we started with a $\rho$ that depends on $\phi$, and differentiated it?

Because the first expression that you wrote as the directed element $d\mathbf{r}$ is not $$d\mathbf{r}=\frac{\partial\mathbf{r}}{\partial {\rho}}d\rho+\frac{\partial\mathbf{r}}{\partial {\phi}}d\phi+\frac{\partial\mathbf{r}}{\partial {z}}dz.$$ One more time, the general expression is $$d\mathbf{r}= d\rho~\hat{\rho}+\rho~d\phi ~\hat{\phi}+dz~\hat z.$$That's the general form for any $\rho$. If $\rho$ is a function of $\phi$ only, i.e. $\rho=g(\phi)$, then $$d\rho=\frac{\partial g}{\partial{\phi}}d\phi$$ and the general expression takes the specific form $$d\mathbf{r}=\frac{\partial g}{\partial{\phi}}d\phi~\hat{\rho}+\rho(\phi)~d\phi ~\hat{\phi}+dz~\hat z=\left[\frac{\partial g}{\partial{\phi}}~\hat{\rho}+g(\phi)~\hat{\phi}\right]d\phi+dz~\hat z.$$ There is no $d\rho$ term in the specific form for $d\mathbf{r}.$ I thought that was obvious when I posted the two specific examples of the circle and ellipse.

Your expression has a $d\rho$ term and that makes it incorrect. You can't have your cake and eat it too. When you say "Consider $\rho=\rho(\phi)$", $\rho$ as a placeholder variable disappears and is replaced by a function of $\phi$. Only the radial unit vector remains.

 

[chiyu]

Your expression has a $d\rho$ term and that makes it incorrect. You can't have your cake and eat it too. When you say "Consider $\rho=\rho(\phi)$", $\rho$ as a placeholder variable disappears and is replaced by a function of $\phi$. Only the radial unit vector remains.

Ohhhh I see now! I think I'm 100% clear now, that makes a lot of sense. Thank you for being patient with me.