Integration of partials, specifically Euler to Bernoulli Equation

[zuppi]

Hi!

I am having trouble following the derivation from Euler's Equation to Bernoulli's Equation. The trouble lies in the math, not the physics part. Especially the step when partial derivatives are being integrated.
I have attached the relevant part as a screenshot.

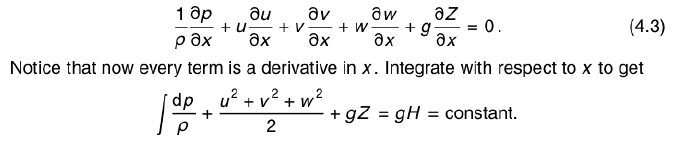
How does the partial dp/dx change into dp? And where does gH come from?

Any help will be much appreciated!

 

[Einj]

You can simply note that, by the chain rule $dp=\frac{\partial p}{\partial x}dx$. As far as gH is concerned, I think it should probably come from your boundary conditions. You need some information to determine the constant.
However, I don't know what H is so I can't really answer your question.

 

[zuppi]

Thanks, that makes sense, I forgot about the chain rule for partials.
Concerning gH I believe it is just another way of expressing the constant to give it a more physical meaning. With H being the "Head" measured in meters. They should have written ... = constant = g*H to make it more clear.

 

[Einj]

Sounds reasonable.