Integration to calculate centre of mass

[MathewsMD]

There are two problems I am facing, and in each one, they are introducing new terms in the integration but I don't understand how.

Problem #1

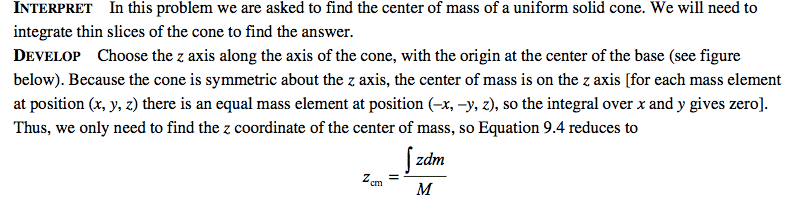
Where I become lost is r=R(1-z/h)
Why is this not just r=R(z/h)? Where does the 1-z come from?

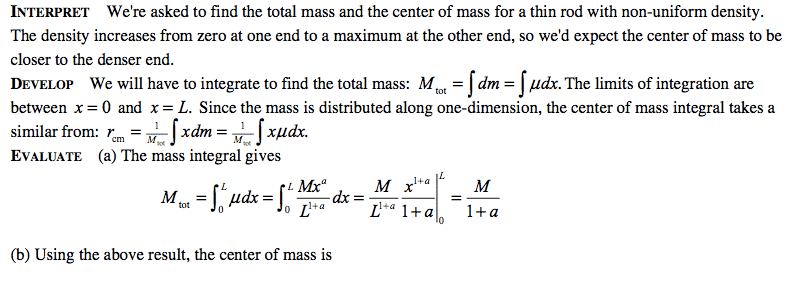
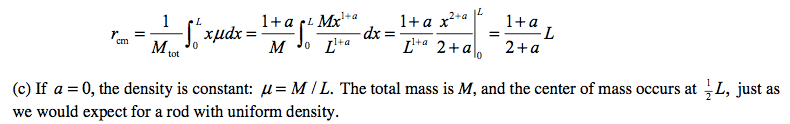
In this question, there is an integration for part b. Where I become confused is when they pull 1+a out of the integral. Where does this 1+a come from? I am relatively new to integration but know the basics. I guess I just can't seem to reason why some of these steps are being done.

Any guidance would be great! :)

 

[Doc Al]

Problem #1

Where I become lost is r=R(1-z/h)
Why is this not just r=R(z/h)? Where does the 1-z come from?

Note that the base of the cone is at z = 0, which is where the radius of the disk will be greatest and equal to R. r is the radius of the disk as a function of z.

 

[SteamKing]

In the diagram, change the y-axis to the z axis and turn 'dy' into 'dz'. Whoever wrote the text and drew the diagram apparently didn't compare notes.

 

[MathewsMD]

Note that the base of the cone is at z = 0, which is where the radius of the disk will be greatest and equal to R. r is the radius of the disk as a function of z.

Okay. I'm still a little confused on how they derived r=R(1-z/h) though. Any more clarification would be very helpful.

Any assistance on the second problem would be great too!

Thanks :)

In the diagram, change the y-axis to the z axis and turn 'dy' into 'dz'. Whoever wrote the text and drew the diagram apparently didn't compare notes.

And yes. I eventually caught on since they introduced z instead of the y in the image. Thanks for pointing it out.

 

[SteamKing]

When z = 0, r = R and when z = h, r = 0. What you want to do is set up a linear interpolation to determine r between these two values of z. If r = R*z/h, then r = 0 when z = 0; or, in other words, the cone would be turned upside down with the pointy end at the bottom.

As far as the rod is concerned, the explanation in the text is lacking in describing what the parameter 'a' is supposed to mean. Since the density of the rod varies with length, 'a' must have something to do with expressing the density ρ as a function of x.

 

[MathewsMD]

When z = 0, r = R and when z = h, r = 0. What you want to do is set up a linear interpolation to determine r between these two values of z. If r = R*z/h, then r = 0 when z = 0; or, in other words, the cone would be turned upside down with the pointy end at the bottom.

As far as the rod is concerned, the explanation in the text is lacking in describing what the parameter 'a' is supposed to mean. Since the density of the rod varies with length, 'a' must have something to do with expressing the density ρ as a function of x.

Okay, that makes sense. I'm just confused as to why there is a 1-z in the solution instead of just ±z (depending on our definition of z=0).

I feel like I'm missing something obvious right now.

 

[SteamKing]

If it helps, draw a sketch.

 

[Yisus77]

Note that the base of the cone is at z = 0, which is where the radius of the disk will be greatest and equal to R. r is the radius of the disk as a function of z.

To add to the top answer: Imagine a 2D cut of the cone: the cone defines a right triangle such tan Q = R /h. But the position of the differential disk defines a second right triangle with same angle: tan Q = r / h'. Where r is the base radius and h' the height of the inner triangle. Now h' the height of the second triangle is h the total height minus z the position of the differential disk : h' = h-z.

Finally : tan Q = (R / h) = (r /h') = (r /h-z) --> r = (R /h) ( h - z) = R (1 - z/h )